专利摘要
本发明提供的一种用于动态稳定控制的多平衡点非线性系统的设计方法,包括:1)建立同步机组模型,并确定类梯度的定义;2)判断同步机组模型的类梯度性;若同步机组模型是混沌的,3)对步骤1)同步机组模型进行控制器设计;4)将步骤3)的控制器进行电力系统动态稳定分析与控制,从而保证整个电力系统的动态稳定性。本发明所利用的动态稳定控制方法没有涉及到之前类似方法中的线性化,因此大大降低了该方法中产生的累积误差。并且对以后的实际工程具有指导作用。
说明书
技术领域
本发明涉及电力系统领域,具体涉及一种用于动态稳定控制的多平衡点非线性系统的设计方法。
背景技术
随着大区互联电网的形成,电力系统的动态安全稳定问题也变得更加复杂,包括大区互联电力系统的动态特性、大区互联电网的运行控制、受端系统的电压稳定性、交直流系统的相互影响等。这些问题使电力系统的安全稳定运行面临新的挑战,也对电力系统安全稳定分析和控制提出了新的要求。然而到目前为止,解决电力系统小扰动动态稳定广域控制的方法由于线性化方法的引入,给控制器设计带来了一定的累积误差。此外,现存大扰动动态稳定广域控制方法大多依赖于时域仿真和简化,并未给出严格的数学证明,也给控制器的设计带来了一定难度。
同步机组是电力系统的重要组成部分,其是否同步与电力系统的动态稳定性有着密切的关系。对于同步机组来说,表征其动力学特性的非线性动力学方程的类梯度性(即全局渐进稳定性)即对应于同步机组的同步特性。为保证电力系统的动态稳定,对于同步机组来说,了解何时会发生持续的混沌振荡及如何避免振荡的发生具有极其重要的意义。其原因在于:一方面,在非线性系统具有混沌吸引子的情况下连续运行会造成同步特性的破坏并导致贵重设备的严重损失;另一方面,混沌振荡会导致有害暂态谐振的永久危害。
近些年,很多相关文献,比如文献一IEEE Transactions on Magnetics,2003,39:2995-2997,Design of permanent magnets to avoid chaos in PM synchronous machines,Gao,Y.& Chau,K.T.;文献二IEEE Trans.on Circ.Sys.I.,1994,41:40-45,Strange attractors in brushless DC motors,Hemati N和文献三IEEE Trans.Power System,2004,19:1918-1924,Hysteresis and bifurcations in the classical model of generator,Subbarao D.and Singh K K,文献中究了同步机组模型的复杂动力学特性,可以由一系列非线性微分方程进行描述。其中,文献一研究了当没有配置合适尺寸永久磁极时PM同步机组的Hopf分叉和混沌现象。文献二中则指出了直流电机的开环动态特性等价于具有混沌特性的Lorenz系统。动态系统中存在多个吸引子说明了动态系统多种控制条件存在的可能性。在理论推导方面,文献四,Non-local methods for pendulum-like feedback systems(Teubner-Texte zur Mathematik Bd.132,B.G.,Teubner Stuttgart-Leipzig),1992,Leonov G A,Reitmann V and Smirnova V B,给出了保证同步机组同步渐进稳定性的频域判据条件。然而,由于频域条件在验证过程中具有一定的难度,还需要进一步对其进行简化。此外,在上述文献中也未提出相应的动态稳定控制器设计方法。
发明内容
针对现有技术的不足,本发明提供一种用于动态稳定控制的多平衡点非线性系统的设计方法,从非线性系统的同步机组模型的稳定性和混沌特性分析出发,利用多平衡点非线性系统时频域分析方法进行控制器设计,所得到的理论结果可避免传统电力系统动态稳定分析中由于线性化引入的累积误差。
本发明提供的一种用于动态稳定控制的多平衡点非线性系统的设计方法,其改进之处在于,所述方法包括如下步骤:
1)建立同步机组模型,并确定类梯度的定义;
2)判断同步机组模型的类梯度性;
3)对步骤1)同步机组模型进行控制器设计;
4)将步骤3)的控制器进行电力系统动态稳定分析与控制。
其中,步骤1)所述建立同步机组模型:
其中,线性部分的传递函数为m×m维的矩阵K(s):
K(s)=CT(A-sI)-1B
将其简化为:
其中
其中,步骤1)所述类梯度的定义为:
当模型(1)t →+∞时,其解
满足X(t,X0)→c,则y称其为是收敛的;
若描述模型(1)的每个解X(t,X0)都收敛,那么模型(1)是类梯度的。
其中,步骤2)所述判断同步机组模型的类梯度性包括:
假设μ1≥0,存在矩阵P=PT使得引理2中的假设条件1)、4)、5)以及下列时域线性矩阵不等式条件
满足,则模型(1)为类梯度的。
其中,步骤3)所述对步骤1)同步机组模型进行控制器设计包括;
选取状态反馈控制器u=Ky进行系统镇定,系统模型表示为
其中,u∈Rm是控制输入,系统的传递函数变为
其中A=A+K;K为控制器参数。
其中,所述控制器参数K的设计方法包括:
假设μ1≥0,且引理2中的假设条件4)、5)以及以下条件满足:
①矩阵 是对角阵;
②存在矩阵W,Q=QT>0使得
那么存在反馈控制器u=Ky使得系统是类梯度的,且控制器参数可由K=WQ-1得出。
其中,所述类梯度性是指全局渐进稳定性。
其中,所述引理2为:
令μ1≥0,且下列条件满足:
[1]矩阵K(0)是对角矩阵;
[2]对于所有ω∈R,都有
[3]
[4]函数f(σ)具有连续二阶导数,且在任何区间(θ1,θ2)内都有f′(σ)≠0;
[5]
那么非线性系统的模型(1)是类梯度的。
与现有技术比,本发明的有益效果为:
本发明考虑了在不同系统参数和初始条件下同步机组模型的全局动态特性,包括类梯度性和混沌特性,并利用多平衡点非线性系统的时频域方法进行反馈控制器设计来保证同步机组的同步特性,从而保证整个电力系统的动态稳定性。本发明所利用的动态稳定控制方法没有涉及到之前类似方法中的线性化,因此大大降低了该方法中产生的累积误差。并且对以后的实际工程具有指导作用。
本发明利用非线性多平衡点系统的时频域处理方法,以线性矩阵不等式形式给出了同步机组类梯度性判定定理,该判据已利用MATLAB工具箱进行验证。
附图说明
图1是本发明提供的σ(t),η(t),y(t)的时域仿真图。
图2是本发明提供的σ(t),η(t),y(t),t∈[1000,1200]的时域仿真图。
图3是本发明提供的y1,y2,y3相空间仿真图。
图4是本发明提供的σ,y1的相平面仿真图。
图5是本发明提供的η,y1的相平面仿真图。
图6是本发明提供的σ(t),η(t),y(t)的时域仿真图。
图7是本发明提供的η,y2,y3相空间图。
图8是本发明提供的控制器作用下σ(t),η(t),y(t)的时域仿真图。
图9是本发明的总流程图。
具体实施方式
下面结合附图对本发明的具体实施方式作进一步的详细说明。
本发明主要思想是先判断系统是否稳定,如果不稳定,通过设计控制器对其进行控制,保证系统的稳定性。
本发明首先利用KYP引理将类梯度性的频域条件进行转化。KYP引理是动态系统分析和反馈控制领域广泛应用的一个基础结论,通过将频域不等式转化为等价的时域线性矩阵不等式(LMI),KYP引理提供了一种系统分析和综合的数值分析方法。基于所得到的时域线性矩阵不等式条件,本发明进一步对闭环系统进行控制器设计保证其类梯度性,并给出相应的控制器参数求解方法。
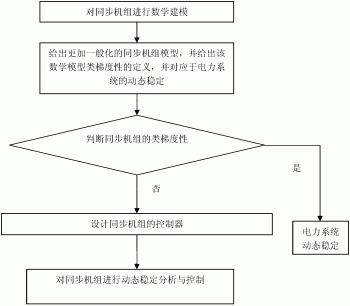
具体的本实施例提供的一种用于动态稳定控制的多平衡点非线性系统的设计方法流程图如图9所示,包括如下步骤:
1)建立同步机组模型,并确定类梯度的定义;
建立同步机组模型:
其中,线性部分的传递函数为m×m维的矩阵K(s):
K(s)=CT(A-sI)-1B
将其简化为:
其中
通过给定不同的参数和初值,系统的模型(3)可以呈现出不同的动力学行为。
在本实施例中,假设
即同步机组模型(1)空载。其中Δ是非线性函数 的周期。
定义1:当系统(1)t→+∞时,系统(1)的解:
满足X(t,X0)→c,则y称其为是收敛的;
定义2:若描述系统的同步机组模型(1)非线性方程的每个解X(t,X0)都收敛,那么模型(1)是类梯度的。
本实施例的类梯度性是指全局渐进稳定性。
2)判断同步机组模型的类梯度性;
引理1:(KYP引理)给定满足det(jwI-A)≠0,w∈R的矩阵A∈Rn×m,矩阵B∈Rn×m以及M=MT∈R(n+m)×(n+m),且(A,B)可控。那么下列两条结论等价:
1°
2°存在矩阵P=PT∈Rn×n使得
即使当(A,B)不可控时,相应不等式也是等价的。
KYP引理给出了频域不等式1°和时域条件2°之间的一种等价关系,它是动力学系统分析、反馈控制和信号处理研究领域中最基本的结论之一。由于动力学系统的性质可由频域中的一系列不等式条件来描述,那么通过KYP引理,可将这类频域条件转化为等价的线性矩阵不等式条件,从而利用相应的工具方便的研究系统的鲁棒性和控制器设计问题。
引理2:令μ1≥0,且下列条件满足:
[1]矩阵K(0)是对角矩阵;
[2]对于所有ω∈R,都有
[3]
[4]函数f(σ)具有连续二阶导数,且在任何区间(θ1,θ2)内都有f′(σ)≠0;
[5]
那么非线性系统(1)是类梯度的。
定理1:假设μ1≥0,存在矩阵P=PT使得引理2中的假设条件1)、4)、5)以及下列LMI条件
满足,则模型(1)为类梯度的。
证明:
首先通过KYP引理对引理2的条件2)进行等价简化。由于
sK(s)=CTA(A-sI)-1-CTB
可以得到
那么引理2的条件2)等价为对于所有的ω∈R都有
Re[CTA(A-iωI)-1-CTB]<0 (6)
此外,由条件3)和K(s)的形式可知,传递函数K(s)中每个元素的分子和分母的阶数差最多是1。因此,由KYP引理可知,不等式(6)成立,当且仅当存在P=PT使得不等式(5)成立。定理得证。
用步骤2)对同步机组进行判断,当判断出同步机组模型是混沌的,则进行步骤3);
3)对步骤1)同步机组模型进行控制器设计;
当系统的模型(1)具有混沌或周期振荡解时,即电网发生动态失稳时,即可在定理1的基础上给出控制器设计方法,从而保证系统的类梯度性(全局渐进稳定性)。本发明选取状态反馈控制器u=Ky来进行系统镇定。此时,系统模型可表示为
其中,u ∈Rm是控制输入,系统的传递函数变为
其中 K为控制器参数。
控制器参数K的设计方法包括:
定理2:假设μ1≥0,且引理2中的假设条件4)、5)以及以下条件满足:
②矩阵 是对角阵;
②存在矩阵W,Q=QT>0使得
那么存在反馈控制器u=Ky使得系统是类梯度的,且控制器参数可由K=WQ-1得出,换句话说,Q是通过求解(8)式得出的一个矩阵,如果(8)式有解,则存在Q,并且控制器K可以通过Q得到。
4)将步骤3)的控制器进行电力系统动态稳定分析与控制,确保电力系统稳定。
具体的,本实施例通过给定不同的参数和初值,模型(3)可以呈现出不同的动力学行为,首先对同步机组不同的动力学行为进行仿真分析。在下列仿真中,统一取初值X(0)=[1.2,0.4,1.0,0.5,1.05]T。
类梯度性:
选择系统参数如下
α1=1.2137,α2=2.1106,α3=7.8436,α4=1.4764
α5=1.0003,α6=6.1205,α7=0.0752,α8=200.04
(10)
α9=0.9037,α10=20.0377,α11=5.4428,α12=1.1826
α13=2.2242
具有上述参数(10)的模型(3)的时域仿真图如图1所示,系统是稳定的。
混沌特性:
取参数
α1=1.1106,α2=2.0871,α3=-9.3000,α4=1.0280
α5=1.0003,α6=6.1205,α7=2.0352,α8=2.0242
(11)
α9=1.9137,α10=2.0377,α11=5.4428,α12=4.1826
α13=2.2242
此时,具有参数(11)的模型(3)的时域仿真曲线如图2-图5所示,此系统是混沌的。
通过计算具有参数(11)下模型(3)的Lyapunov指数,得到
λ1=0.796,λ2=0.000,λ3=2.536
λ4=4.472,λ5=-19.986
其中存在正的Lyapunov指数λ1=0.796说明了系统的混沌特性。由于在非线性电力系统具有混沌吸引子的情况下连续运行会造成同步特性的破坏并导致贵重设备的严重损失,从而对电网的动态稳定性造成严重威胁。此外,混沌振荡会导致有害暂态谐振的永久危害,因此对于同步机组来说如何避免混沌振荡的发生具有极其重要的意义。换句话说,为保证电力系统的动态稳定性,需要设计适当的控制器对同步机组进行控制。在上述给出系统初值进行仿真结果的基础上,下步用仿真结果证实按照本发明所设计的动态稳定控制器的有效性。
在本实施步骤中,再选取初值X(0)=[2.2,4,1.0,1.5,2.5]T。那么具有系统参数
α1=1.1106,α2=2.1271,α3=9.0000,α4=1.0280
α5=1.0003,α6=6.1205,α7=2.0352,α8=200.0
α9=-1.9122,α10=0.0377,α11=5.4428,α12=20.0,α13=2.2242
的同步机组模型(3)的动力学特性由图6、图7进行描述。
从图6、图7不难看出,此时同步机组模型(3)具有典型的非线性混沌特性,相应的,由系统(3)构成的电力系统发生动态失稳。下面考虑在控制器u=Ky作用下的闭环系统特性。显然,此时引理2中的条件4)、5)都满足。通过求解定理2中的LMI条件(8),可以得到如下的状态反馈控制器:
从而由定理2可知保证了系统的类梯度性。
为验证所得理论结果的有效性,图8中给出了系统在控制器(9)作用下的系统稳定仿真曲线,图形结果也再一次验证同步机组模型(3)达到了全局渐进稳定,从而保证了电力系统的动态稳定。
需要说明的是,本发明的各个字母物理意义如下:
σ、η、y都对应于同步机组中的物理参数,是随时间变化的向量,其中向量y=[y1,y2,y3]T;
A、B、C是同步机组模型中的已知参数矩阵,是常数矩阵;
c为任意常数;
f(σ)、 g(η,σ)是同步机组模型中关于σ的周期非线性函数;
α为一般化的同步机组模型中的已知参数;
u为同步机组中的控制输入变量;
X0是σ0、η0、y0组成的初值列向量,且有:
σ0、η0、y0分别是σ、η、y的初值;
分别是σ、η、y随时间的导数;
α1-α13为方程系数;
为变换后的传递函数;
为变换后的矩阵,
本发明提供的KYP引理出自Syst.Contr Lett.1996,28:7-10.On the Kalman-Yakubovich-Popov lemma,Rantzer A。
本发明提供的引理2出自1992.,Non-local methods for endulum-like feedback systems (Teubner-Texte zur Mathematik Bd.132,B.G.,Teubner Stuttgart-Leipzig),Leonov G A,Reitmann V and Smirnova VB。
最后应当说明的是:以上实施例仅用以说明本发明的技术方案而非对其限制,尽管参照上述实施例对本发明进行了详细的说明,所属领域的普通技术人员应当理解:依然可以对本发明的具体实施方式进行修改或者等同替换,而未脱离本发明精神和范围的任何修改或者等同替换,其均应涵盖在本发明的权利要求范围当中。
一种用于动态稳定控制的多平衡点非线性系统的设计方法专利购买费用说明
![]()
Q:办理专利转让的流程及所需资料
A:专利权人变更需要办理著录项目变更手续,有代理机构的,变更手续应当由代理机构办理。
1:专利变更应当使用专利局统一制作的“著录项目变更申报书”提出。
2:按规定缴纳著录项目变更手续费。
3:同时提交相关证明文件原件。
4:专利权转移的,变更后的专利权人委托新专利代理机构的,应当提交变更后的全体专利申请人签字或者盖章的委托书。
Q:专利著录项目变更费用如何缴交
A:(1)直接到国家知识产权局受理大厅收费窗口缴纳,(2)通过代办处缴纳,(3)通过邮局或者银行汇款,更多缴纳方式
Q:专利转让变更,多久能出结果
A:著录项目变更请求书递交后,一般1-2个月左右就会收到通知,国家知识产权局会下达《转让手续合格通知书》。
动态评分
0.0