专利摘要
本发明提供了一种滚子推杆等加速度直动时移动凸轮廓线的求解方法,以克服目前该类移动凸轮机构设计中凸轮轮廓曲线的求解缺乏参考方法、凭经验设计等不足。该求解方法形成的凸轮廓线包括上升段抛物线EN与NF、水平段直线FFf、下降段抛物线FfNf与NfEf,连接以上各段得到移动凸轮的轮廓曲线。本发明的有益效果是:根据所提供的方法求出的移动凸轮轮廓,在滚子推杆作等加速度往复直线运动时,推杆的运动速度无突变,消除了凸轮机构的刚性冲击,降低了传动件的振动与噪声,从而延长了凸轮机构的寿命;所述移动凸轮廓线求解方法简单直观、易于掌握,求出的凸轮廓线光滑连续、不会出现尖点或失真现象,便于用数控机床加工,生产效率高。
权利要求
1.一种滚子推杆等加速度直动时移动凸轮廓线的求解方法,所述移动凸轮指与其匹配的滚子推杆作等加速度直动时的凸轮;其特征在于,该求解方法形成的移动凸轮廓线包括上升段抛物线EN与NF、水平段直线FFf、下降段抛物线FfNf与NfEf,所述移动凸轮廓线的具体求解步骤如下:
1)根据设计工况要求拟定:滚子推杆的升程H、滚子推杆作等加速度直动时的加速度a、凸轮的移动速度V、与滚子推杆的升程H对应的凸轮位移L1,与水平段直线FFf对应的凸轮位移L2;
2)按照滚子推杆的运动速度无突变、凸轮廓线光滑连续且不存在尖点或失真的原则,联立方程(1)与(2):
得到滚子推杆的滚子半径r、凸轮廓线上升段抛物线EN与NF的连接点的横坐标xN;
3)分别建立凸轮廓线的上升段抛物线、水平段直线、下降段抛物线的数学方程式:
①建立凸轮廓线的上升段抛物线EN,其数学方程为:
②建立凸轮廓线的上升段抛物线NF,其数学方程为:
③建立凸轮廓线的水平段直线FFf,其数学方程为:
④建立下降段抛物线FfNf与NfEf对应的数学方程:
FfNf是将抛物线NF沿FFf的中心线镜像后得到的抛物线,NfEf是将抛物线EN沿FFf的中心线镜像后得到的抛物线;
4)连接上升段抛物线EN与NF、水平段直线FFf、下降段抛物线FfNf与NfEf,得到滚子推杆作等加速度直动时的移动凸轮廓线。
说明书
技术领域
本发明涉及一种凸轮廓线的求解方法,具体涉及一种滚子推杆作等加速度直动时移动凸轮廓线的求解方法,属于凸轮机构设计技术领域。
背景技术
凸轮是能控制从动件运动规律的具有曲线轮廓的构件,含有凸轮的机构称为凸轮机构。凸轮机构结构简单紧凑、占据空间小、工作可靠,对于几乎任意要求的从动件的运动规律,都可以设计出凸轮廓线来实现。因此,凸轮机构已经成为各种机械,特别是自动机械和自动控制装置中的一种常用机构,尤其在高速、高精度传动与分度机构及引导机构中,具有无可替代的优越性。凸轮的廓线和从动件一起实现运动形式的转换,凸轮廓线的设计和制造方法的研究对于现代制造业具有重要的意义。
凸轮按形状分,有盘形凸轮、移动凸轮、圆柱凸轮三种,盘形凸轮是凸轮的最基本型式,教科书及有关手册里叙述的最多,应用领域也最为广泛。移动凸轮是盘形凸轮的一个特例,它可以看作转动中心在无穷远处的盘形凸轮,移动凸轮在靠模车削机构、录音机卷带机构等机构中都有应用。
移动凸轮机构研发的关键是移动凸轮廓线的设计,移动凸轮廓线的形状决定着与之匹配的从动件的性能,然而,国内近二十年来的有关机械设计手册或书籍中很少涉及移动凸轮廓线设计方面的内容。针对滚子推杆(从动件)作等加速度往复直线运动时移动凸轮廓线的求解,迄今国内外尚未出现直接的分析指导方法。工程技术人员在设计该类移动凸轮廓线时,往往是借鉴并套用盘形凸轮的有关公式,设计过程有赖于经验,而且往往不能同时兼顾凸轮机构的冲击、凸轮廓线光滑连续与运动失真等问题。
发明内容
为了克服现有技术的不足,本发明提供了一种求解过程直观、易于掌握的滚子推杆作等加速度往复直动时移动凸轮廓线的求解方法,以解决目前该类移动凸轮机构设计中凸轮廓线的求解缺乏参考方法或者凭经验求解而带来的困难及设计不合理等问题。
本发明的目的通过以下技术方案来实现:
一种滚子推杆等加速度直动时移动凸轮廓线的求解方法,所述移动凸轮指的是与其匹配的滚子推杆作等加速度直动时的凸轮,移动凸轮的升程可以用滚子推杆的升程来表述,滚子推杆的位移函数定义为当凸轮平移x时,滚子推杆从初始位置上升了位移y,即移动凸轮廓线可以表述成凸轮位移x的函数;该求解方法形成的移动凸轮廓线包括上升段抛物线EN与NF、水平段直线FFf、下降段抛物线FfNf与NfEf,所述移动凸轮廓线的具体求解步骤如下:
1)根据设计工况要求拟定:滚子推杆的升程H、滚子推杆作等加速度直动时的加速度a、凸轮的移动速度V、与滚子推杆的升程H对应的凸轮位移L1,与水平段直线FFf对应的凸轮位移L2;
2)按照滚子推杆的运动速度无突变、凸轮廓线光滑连续且不存在尖点或失真的原则,联立方程(1)与(2):
得到滚子推杆的滚子半径r、凸轮廓线上升段抛物线EN与NF的连接点的横坐标xN;
3)分别建立凸轮廓线的上升段抛物线、水平段直线、下降段抛物线的数学方程式:
①建立凸轮廓线的上升段抛物线EN,其数学方程为:
②建立凸轮廓线的上升段抛物线NF,其数学方程为:
③建立凸轮廓线的水平段直线FFf,其数学方程为:
④建立下降段抛物线FfNf与NfEf对应的数学方程:
FfNf是将抛物线NF沿FFf的中心线镜像后得到的抛物线,NfEf是将抛物线EN沿FFf的中心线镜像后得到的抛物线;
4)连接上升段抛物线EN与NF、水平段直线FFf、下降段抛物线FfNf与NfEf,得到滚子推杆作等加速度直动(直线往复运动)时的移动凸轮廓线。
本发明具有如下有益效果:
(1)所提供的移动凸轮廓线求解方法简单通用,可操作性好,易于掌握。只要按照所述步骤设计出移动凸轮的轮廓曲线,滚子推杆(从动件)就能实现预定的运动规律---等加速度往复直线运动。
(2)所得到的移动凸轮轮廓曲线光滑连续,不会出现尖点或运动失真现象。在滚子推杆作等加速度往复直线运动时,避免了推杆运动速度的突然变化,消除了凸轮机构的刚性冲击,减轻了传动件的振动,能够有效地降低噪声,从而延长凸轮机构的寿命。
(3)求出的凸轮廓线,便于用数控机床加工,确保加工出精度满足要求、质量稳定的凸轮,生产效率大大提高。
附图说明
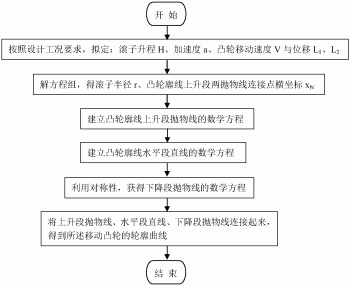
图1是本发明滚子推杆等加速度直动时移动凸轮廓线的求解方法实施例的流程图;
图2为本发明所述求解方法形成的移动凸轮廓线及与其匹配的滚子推杆作等加速度往复直线运动时的滚子中心轨迹之间的关系示意图;
图3为本发明滚子推杆等加速度直动时移动凸轮廓线的求解方法形成的移动凸轮外形结构示意图。
图中:EN与NF为上升段抛物线、FFf为水平段直线、FfNf与NfEf为下降段抛物线,RP表示滚子,r为滚子半径,H为滚子推杆的升程、L1为与滚子推杆的升程H对应的凸轮位移,L2为与水平段直线FFf对应的凸轮位移,ENFFfNfEf为移动凸轮的轮廓曲线,OMTTfMfOf为滚子沿着凸轮廓线作往复直线运动时的滚子中心轨迹。
具体实施方式
下面结合附图,详细描述本发明移动凸轮廓线求解方法的实施过程。
1)启动系统;
2)根据设计工况或生产现场实际要求,拟定滚子推杆的升程H、滚子推杆作等加速度直动时的加速度a、凸轮的移动速度V、与滚子推杆的升程H对应的凸轮位移L1,与水平段直线FFf对应的凸轮位移L2;
3)兼顾移动凸轮廓线光滑连续且不存在尖点或失真现象,同时考虑滚子推杆的运动速度不发生突然变化的要求,联立求解方程(1)与(2),得到滚子推杆的滚子半径r、凸轮廓线上升段抛物线EN和NF的连接点的横坐标xN:
4)分别建立与凸轮廓线的上升段、水平段、下降段对应的数学方程式:
①根据公式(3)建立凸轮廓线的上升段抛物线EN的数学方程:
②按照公式(4)得到凸轮廓线的上升段抛物线NF的数学方程:
③根据公式(5)建立凸轮廓线的水平段直线FFf的数学方程:
④利用对称性,获得下降段抛物线FfNf与NfEf对应的数学方程:
将抛物线NF沿FFf的中心线镜像后得到抛物线FfNf,将抛物线EN沿FFf的中心线镜像后得到抛物线NfEf;
5)将上述求得的上升段抛物线EN与NF、水平段直线FFf、下降段抛物线FfNf与NfEf光滑连接起来,便可得到滚子推杆作等加速度直动时的移动凸轮的轮廓曲线,完成所述移动凸轮廓线的求解工作。
为了体现本发明移动凸轮廓线求解方法的简单易行,下面通过一个具体的设计过程加以说明。
已知某直动滚子推杆移动凸轮机构的从动件输出端按“升--停--回”的运动特征作往复直线运动,升程和回程段凸轮均作匀速移动,滚子推杆的运动加速度是常值。
首先:根据设计工况及用户要求,确定滚子推杆的升程H=50mm,滚子推杆的运动加速度a=6.5mm/s2,凸轮的移动速度V=25mm/s、与滚子推杆的升程H对应的凸轮位移L1=150mm,与水平段直线FFf对应的凸轮位移L2=50mm。
求解该移动凸轮的轮廓曲线,可通过以下步骤实现:
1)将滚子推杆、移动凸轮的上述已知参数值代入方程(1)与(2),得到:
联立求解这两个方程得:滚子推杆的滚子半径r=36.0299mm、凸轮廓线上升段抛物线EN和NF的连接点的横坐标xN=85.0805mm;
2)根据公式(3)得到凸轮廓线上升段抛物线EN的数学方程为:
3)按照公式(4)得到凸轮廓线上升段抛物线NF的数学方程为:
4)根据公式(5)得到凸轮廓线水平段直线FFf的数学方程为:
此时,滚子推杆(从动件)进入远休止状态。
5)利用对称性原理,将抛物线NF沿FFf的中心线镜像后得到抛物线FfNf的数学方程为:
将抛物线EN沿FFf的中心线镜像后得到抛物线NfEf的数学方程如下:
6)根据上面求得的各个方程,可以分别绘制出上升段抛物线EN与NF、水平段直线FFf、下降段抛物线FfNf与NfEf,将这些线光滑连接起来,便可得到滚子推杆作等加速度直动时的移动凸轮的轮廓曲线,从而结束所述移动凸轮廓线的求解过程。
本发明的移动凸轮廓线求解方法是依据移动凸轮廓线光滑连续且不存在尖点或失真现象、滚子推杆的运动速度不发生突变等要求来求解凸轮廓线。尽管结合附图对本发明进行了上述描述,但是本发明并不局限于上述的具体实施方式,上述的具体实施方式仅仅是示意性的,而不是限制性的。凡是采用本发明的相似方法及其相似变化,均应列入本发明的保护范围。
滚子推杆等加速度直动时移动凸轮廓线的求解方法专利购买费用说明
![]()
Q:办理专利转让的流程及所需资料
A:专利权人变更需要办理著录项目变更手续,有代理机构的,变更手续应当由代理机构办理。
1:专利变更应当使用专利局统一制作的“著录项目变更申报书”提出。
2:按规定缴纳著录项目变更手续费。
3:同时提交相关证明文件原件。
4:专利权转移的,变更后的专利权人委托新专利代理机构的,应当提交变更后的全体专利申请人签字或者盖章的委托书。
Q:专利著录项目变更费用如何缴交
A:(1)直接到国家知识产权局受理大厅收费窗口缴纳,(2)通过代办处缴纳,(3)通过邮局或者银行汇款,更多缴纳方式
Q:专利转让变更,多久能出结果
A:著录项目变更请求书递交后,一般1-2个月左右就会收到通知,国家知识产权局会下达《转让手续合格通知书》。
动态评分
0.0