专利摘要
本发明公开了一种三连杆式并联结构机器人正解确定方法,所述三连杆式并联结构机器人的结构主要由运动平台(1)、三个连杆(、、)和三个立柱(2)组成,所述运动平台(1)通过三个球铰(、、)分别与三个连杆(、、)连接,三个连杆(、、)通过三个圆柱铰(、、)与三个滑座(3)相连,三个滑座(3)在三个立柱(2)上做垂直滑动,三个球铰(、、)呈正三角形,本发明采用蒙特卡洛方法进行初始解的随机设置,通过大量的随机抽样得到所有可能的解,然后绘制运动平台位姿简图,以此直观方便地判断解的合理性。本发明对3-PRS并联机器人工作空间的设计、分析及优化,促进其在工业生产的广泛应用,具有重要的学术意义及实用价值。
权利要求
1.一种三连杆式并联结构机器人正解确定方法,其特征在于,所述三连杆式并联结构机器人的结构主要由运动平台(1)、三个连杆( 、 、 )和三个立柱(2)组成,运动平台(1)通过三个球铰( 、 、 )分别与三个连杆( 、 、 )连接,三个连杆( 、 、 )通过三个圆柱铰( 、 、 )与三个滑座(3)相连,三个滑座(3)在三个立柱(2)上做垂直滑动,
三个连杆( 、 、 )的长度分别为 、 、 ,
三个球铰( 、 、 )呈正三角形,其外接圆半径为 ,
三个立柱(2)在水平面内的投影( 、 、 )呈正三角形,其外接圆半径为 ,
三个连杆( 、 、 )与三个立柱(2)之间的夹角分别为 、 、 ,
固定坐标系OXYZ建立于与三个立柱 (2) 固连的基座上,坐标原点O置于三角形 的中心,X轴过点 ,Y轴沿 方向,
三个滑座(3)的高度为 ,
所述三个球铰( 、 、 )的坐标用向量的形式可表示为
(a)
其中, 、 、 的关系为:
(b)
所述正解确定方法包括如下步骤:
Step 1:设置三连杆式并联结构机器人的基本参数:
包括三个连杆( 、 、 )的长度 、 、 ,运动平台(1)的外接圆半径 ,三个立柱(2)的投影( 、 、 )的外接圆半径 ,三个滑座(3)的高度 ,每个连杆与相连立柱之间的夹角 、 、 的范围,归并相同解时三个夹角 、 、 的精度 ,确定迭代初始值的概率分布规律;
Step 2:求可行解,将其存储于数组 、 、 中;
Step 3:归并相同解;
Step 4:保存数据,根据归并后的每个解绘制三连杆式并联结构机器人的简图,判断解的合理性,进而确定正解;
Step 5:结束。
2.如权利要求1所述的三连杆式并联结构机器人正解确定方法,其特征在于,所述步骤Step 2中,设定了两个量 和 来控制可行解求解的规模, 为欲得到方程(b)解的个数, 为蒙特卡洛方法抽样次数的上限。
3.如权利要求1或2所述的三连杆式并联结构机器人正解确定方法,其特征在于,所述步骤Step 2中,首先循环变量赋初值 , ,然后求解过程开始,包括如下步骤:
Step 2.1:确定优化迭代的初始值,
Step 2.2:通过优化迭代求解方程(b)一次,得到一组解 、 、 ,
Step 2.3: ,
Step 2.4:如果求得的 、 、 超出了Step 1中设定的范围或者超出了三连杆式并联结构本身的限制,则转Step2.5,
否则, ,保存解 , , ,转Step3.5,
Step 2.5:判断是否满足退出条件,如果满足,则转Step 3,否则转Step 2.1。
4.如权利要求3所述的三连杆式并联结构机器人正解确定方法,其特征在于,所述步骤Step 2.1中,优化迭代的初始值是根据Step 1中设定的概率分布规律通过蒙特卡洛方法抽样得到。
5.如权利要求3所述的三连杆式并联结构机器人正解确定方法,其特征在于,所述步骤Step 2.5中,退出条件为: 或 。
6.如权利要求1所述的三连杆式并联结构机器人正解确定方法,其特征在于,所述步骤Step 3中,归并相同解中,包括如下步骤:
Step 3.1:循环变量 ,
Step 3.2:循环变量 ,
Step 3.3:当
(c)
时,转Step 3.4,否则转Step 3.5,
Step 3.4:认为第 两个解属同一个解,删除第 个解,后面的解依次前移, ,转Step3.6,
Step 3.5: ,
Step 3.6:如果 ,转Step 3.3,否则转Step 3.7,
Step 3.7: ,如果 ,转Step 3.2,否则,解的归并结束,转Step 4。
说明书
技术领域
本发明涉及一种三连杆式并联结构机器人正解确定方法,属于机器人机构学领域。
背景技术
三自由度的3-PRS (P为移动副,R为转动副,S为球面副) 并联结构机器人由三个对称的支链组成,每个支链都有一个连杆,它是[PP]S类并联机构的典型结构之一,具有结构简单、刚性大、承载能力高、结构紧凑等优点。尽管只有3个运动自由度,但是与其他机构进行配合,如下设二维运动平台,则可扩充自由度并增大工作空间,因此具有广阔的应用前景,得到了世界各国学术界及工业界的广泛关注。3-PRS并联结构机器人反解容易获得,可以得到显性的解析表达式;但是正解的显性解析表达式求解十分困难。求正解的方程组是一个包含三个未知量的非线性方程组,并且包含了角度的三个函数。通过三角函数万能公式进行代换,可以得到16次的多项式方程组,共有64组可能的解,推导与计算过程繁琐。用连续同伦方法计算3-PRS并联结构机器人的正解,可减小正解数值求解过程中由于初始值设置不当和迭代方法引起的问题; Bezout消元法、优化方法、遗传算法等都可用来计算数值正解。但是正解数值计算方法中,只要采用了非线性方程的迭代解或优化算法,都可能因初始值、真实解的区间及优化方法设置不合理导致求解失败或漏掉真实解。
发明内容
针对上述的问题,本发明目的在于提供一种三连杆式并联结构机器人正解确定方法,采用蒙特卡洛方法进行初始解的随机设置,通过大量的随机抽样得到所有可能的解,然后绘制运动平台位姿简图,以此直观方便地判断解的合理性。本发明对3-PRS并联结构机器人工作空间的设计、分析及优化,促进其在工业生产的广泛应用,具有重要的学术意义及实用价值。
本发明为解决上述技术问题所采用的技术方案如下所描述:
一种三连杆式并联结构机器人正解确定方法,所述三连杆式并联结构机器人的结构主要由运动平台、三个连杆( 、 、 )和三个立柱组成,所述运动平台通过三个球铰( 、 、 )分别与三个连杆( 、 、 )连接,三个连杆( 、 、 )通过三个圆柱铰( 、 、 )与三个滑座相连,三个滑座在三个立柱上做垂直滑动,
三个连杆( 、 、 )的长度分别为 、 、 ,
三个球铰( 、 、 )呈正三角形,其外接圆半径为 ,
三个立柱在水平面内的投影( 、 、 )呈正三角形,其外接圆半径为 ,
三个连杆( 、 、 )与三个立柱之间的夹角分别为 、 、 ,
固定坐标系OXYZ建立于与三个立柱固连的基座上,坐标原点O置于三角形 的中心,X轴过点 ,Y轴沿 方向,
三个滑座的高度为 ,
所述三个球铰( 、 、 )的坐标用向量的形式可表示为
(a)
其中, 、 、 的关系为:
(b)
其特征在于,所述正解确定方法包括如下步骤:
Step 1:设置三连杆式并联结构机器人的基本参数:
包括三个连杆( 、 、 )的长度 、 、 ,运动平台的外接圆半径 ,三个立柱的投影( 、 、 )的外接圆半径 ,三个滑座的高度 ,每个连杆与相连的立柱之间的夹角 、 、 的范围,归并相同解时三个夹角 、 、 的精度 ,确定迭代初始值的概率分布规律;
Step 2:求可行解,将其存储于数组 、 、 中;
Step 3:归并相同解;
Step 4:保存数据,根据归并后的每个解绘制三连杆式并联结构机器人的简图,判断解的合理性,进而确定正解;
Step 5:结束。
进一步,所述步骤Step 2中,设定了两个量 和 来控制可行解求解的规模, 为欲得到方程(b)解的个数, 为蒙特卡洛方法抽样次数的上限。
进一步,所述步骤Step 2中,首先循环变量赋初值 , ,然后求解过程开始,包括如下步骤:
Step 2.1:确定优化迭代的初始值,
Step 2.2:通过优化迭代求解方程(b)一次,得到一组解 、 、 ,
Step 2.3: ,
Step 2.4:如果求得的 、 、 超出了Step 1中设定的范围或者超出了三连杆式并联结构本身的限制,则转Step2.5,
否则, ,保存解 , , ,转Step2.5,
Step 2.5:判断是否满足退出条件,如果满足,则转Step 3,否则转Step 2.1。
进一步,所述步骤Step 2.1中,优化迭代的初始值是根据Step 1中设定的概率分布规律通过蒙特卡洛方法抽样得到。
进一步,所述步骤Step 2.5中,退出条件为: 或 。
再进一步,所述步骤Step 3中,归并相同解中,包括如下步骤:
Step 3.1:循环变量 ,
Step 3.2:循环变量 ,
Step 3.3:当
(c)
时,转Step 3.4,否则转Step 3.5,
Step 3.4:认为第 两个解属同一个解,删除第 个解,后面的解依次前移, ,转Step3.6,
Step 3.5: ,
Step 3.6:如果 ,转Step 3.3,否则转Step 3.7,
Step 3.7: ,如果 ,转Step 3.2,否则,解的归并结束,转Step 4。
本发明的有益效果如下:本发明充分利用了蒙特卡洛方法的随机性进行初始值的随机设置,首先通过大量的随机抽样得到3-PRS并联结构机器人正解方程所有可能的解,在较少的抽样次数下搜索到所有解,然后绘制运动平台位姿简图,以此直观方便地判断解的合理性。由于蒙特卡洛抽样的随机性,即便是相同的参数,程序先后两次运行得到的结果也不完全相同,但是差异都只是小数点后最后几位数字,因此本发明所提供的方法具有很高的精度。另外,本发明所求出的数值解中共包含了不合理的解,本发明又通过编程在对解进行初步判断的基础上,剔除了部分明显不合理的解,根据剩下的解绘制3-PRS并联机构机器人运动平台的位姿简图,可以直观地判断解的合理性。因此,本发明对3-PRS并联机器人工作空间的设计、分析及优化,促进其在工业生产的广泛应用,具有重要的学术意义及实用价值。
附图说明
图1为3-PRS并联机构机器人的三维结构示意图;
图2为3-PRS并联机构机器人的俯视图;
图3为算例1解对应的运动平台位姿;
图4为算例4解对应的运动平台位姿。
具体实施方式
下面结合附图和具体实施例来对本发明进行描述。
如图1、2所示,固定坐标系OXYZ建立于与三个立柱2固连的基座上,坐标原点O置于三角形 的中心,X轴过点 ,Y轴沿 方向。三个连杆 、 、 的长度为 、 、 ,三个连杆与三个立柱2之间的夹角分别为 、 、 。则三个球铰 、 、 的坐标用向量的形式可表示为
(1)
由三个球铰 为正三角形,所以有
(2)
根据式(2)可以求得三个夹角 、 、 ,将三个角度代入式(1)可得 、 、 的坐标,由此可计算得到运动平台1的姿态及中心的坐标。如运动平台1中心的三维坐标向量为
(3)
但是式(2)中包含了三角函数,并且又是一个非线性高次方程,所以解析表达式求解非常困难。求其数值解不失为很好的选择,但是由于数值解通常是通过优化的方法进行迭代求解,迭代初始值的设定严重影响解的个数及精度,如果初始解设置的不合适,可能漏解,甚至漏掉满足机构约束条件的真实解。
为了克服初始解设置不当引起求解失败的问题,本发明提出了用蒙特卡洛方法设置迭代初始值,其过程可以描述如下:
Step 1:设置3-PRS并联结构机器人的基本参数。包括三个连杆( 、 、 )的长度 、 、 ,运动平台1的外接圆半径 ,三个立柱2的投影( 、 、 )的外接圆半径 ,三个滑座3的高度 ,每个连杆与相连的立柱之间的夹角 、 、 的范围,归并相同解时三个夹角 、 、 的精度 ,确定迭代初始值的概率分布规律。
Step 2:设定欲得到方程(2)解的个数 ,蒙特卡洛方法抽样的次数的上限 ,求解过程开始,循环变量 , 。
Step 2.1: 初始值抽样。根据设定的概率分布规律生成表示 、 、 初始值的随机数。
Step 2.2: 用随机生成的初始值,通过优化迭代求解方程(2)一次,得到一组解 、 、 。
Step 2.3: 。
Step 2.4: 如果求解不成功,或者求得的 、 、 超出了设定的范围或超出了3-PRS并联结构机器人的约束条件,则转Step2.5;否则 ,保存解 , , ,转Step2.5。
Step 3.5: 如果 或 ,则转Step 3;否则转Step 2.1。
Step 3:归并相同解。
Step 3.1:循环变量 。
Step 3.2:循环变量 。
Step 3.3:当
(4)
时,转Step 3.4;否则转Step 3.5。
Step3.4:认为第 两个解属同一个解,删除第 个解;后面的解依次前移, 。转Step3.6。
Step3.5: 。
Step3.6:如果 ,转Step 3.3;否则转Step 3.7。
Step3.7: 。如果 转Step3.2;否则,解的归并结束,转Step 4。
Step 4:保存数据,根据归并后的每个解绘制三连杆式并联结构机器人的简图,判断解的合理性,进而确定正解。
Step 5:结束。
下面用具体的算例来验证本发明提供的技术方案的正确性与有效性。
【算例1】设3-PRS并联结构机器人的参数为: , , , , , 、 、 的范围为 。设定 , 。在抽样400次,每次都能收敛到方程(2)的解,并且迭代精度控制在
得到的400个解以 的精度进行归并,最终得到8个解,如表1所示。从本算例中给定的3-PRS并联结构机器人的参数来看,机构是对称的。但从直观上来看,8个数值解中,第4、5两个合理性较高。8个解对应的平台位姿如图3所示。从图中可以明显看到,第4个解对应于平台的正常位姿,是合理的解;第5个解平台翻转了180°,三个连杆出现干涉,则为不合理的解;其他6个解对应的平台位置都不是正常的位姿,要么平台翻转,要么连杆干涉。所以,只有第4个解是正确的解。实际上,这8个解可以分为4组:4与5,1与2,3与8,6与7。4与5平台位姿是180°翻转关系,其他3组都是对称的。由于三个圆柱铰的限制, 、 、 的运行被限定在相应的空间平面 : , : 和 : 。如果限定 、 、 运动的极限位置为这3个平面的交线,则可避免平台翻转及连杆干涉。在此限定下,重新计算。则只得到第4个解。
表1 【算例1】的解
【算例2】将算例1中三个连杆的长度改为 ,也可得到8个解,如表2所示。如果绘制出平台位姿简图,可以发现仍是第4个解为合理的解,平台位姿与图3d)相似。
表2 【算例2】的解
【算例3】将算例1、算例2与中三个连杆的长度继续缩小,取 ,只得到一个解(19.471220634490681,19.471220634490695,19.471220634490695),平台位姿与图3d)相似。如果再继续缩短连杆的长度,当其短到某一个临界值之后,方程无解。这个临界值可以通过机构的极限位置得到。因为上面三个算例中限定了三个角度的最大值为 ,则三个连杆的临界长度为 。
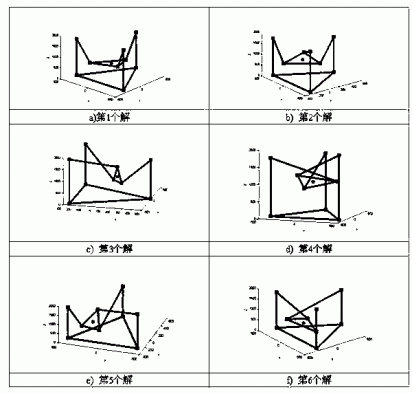
【算例4】将算例1中三个滑座的高度变为 , , 。则可得到如表3所示的6个解,对应的平台位姿如图4所示,第1个为合理的解。如果限定 、 、 运动的极限位置为平面 、 与 的公共交线,重新计算,则只得到第1个解。
表3 【算例4】的解
在上面的4个算例中,最终得到的解保留了15位小数。由于蒙特卡洛抽样的随机性,即便是相同的参数,程序先后两次运行得到的结果不完全相同,但是差异都只是小数点后最后几位数字,可见本发明的方法具有很高的精度。由于本发明提出的解法,没有对非线性方程(2)做任何数学特性的分析,为了避免初始值设置不当导致求解失败,设置了蒙特卡洛方法抽样的次数上限 。实际上,上面的4个算例中,每次抽样得到的初始值最终都收敛到方程(2)的解。 与 值设置的越大,搜索到所有解的概率就越大,当 时得到的结果与 时一样,可见本发明的方法在较少的抽样次数下就可找到所有的解。非线性方程(2)解的个数严重依赖于3-PRS并联结构机器人的参数以及滑座3的位置,而且产生了不合理的解。如果不直观地观察运动平台1的位姿简图,单纯从三个角度的范围无法确切判断解的合理性。因此,如果要在程序中自动判断解的合理性,必须根据3-PRS并联结构机器人的具体参数分析末端位姿的极限范围。
需要注意的是,上述具体实施例仅仅是示例性的,在本发明的上述教导下,本领域技术人员可以在上述实施例的基础上进行各种改进和变形,而这些改进或者变形均落在本发明的保护范围内。本领域技术人员应该明白,上面的具体描述只是为了解释本发明的目的,并非用于限制本发明。本发明的保护范围由权利要求及其等同物限定。
三连杆式并联结构机器人正解确定方法专利购买费用说明
![]()
Q:办理专利转让的流程及所需资料
A:专利权人变更需要办理著录项目变更手续,有代理机构的,变更手续应当由代理机构办理。
1:专利变更应当使用专利局统一制作的“著录项目变更申报书”提出。
2:按规定缴纳著录项目变更手续费。
3:同时提交相关证明文件原件。
4:专利权转移的,变更后的专利权人委托新专利代理机构的,应当提交变更后的全体专利申请人签字或者盖章的委托书。
Q:专利著录项目变更费用如何缴交
A:(1)直接到国家知识产权局受理大厅收费窗口缴纳,(2)通过代办处缴纳,(3)通过邮局或者银行汇款,更多缴纳方式
Q:专利转让变更,多久能出结果
A:著录项目变更请求书递交后,一般1-2个月左右就会收到通知,国家知识产权局会下达《转让手续合格通知书》。
动态评分
0.0