专利摘要

本发明属于阵列信号处理技术领域，尤其涉及基于互质面阵的二维波达方向快速估计方法。基于互质面阵的二维波达方向快速估计方法，包括以下步骤：根据互质面阵模型，分x轴和y轴构造阵列流型矩阵；所述互质面阵模型由两个均匀稀疏面阵组合而成；分别求解各子阵接收信号的协方差矩阵，并分x轴和y轴方向构造阵列的传播算子矩阵；在对阵列流型进行分块处理的基础上采用PM算法，分别求取各个子阵沿x轴和y轴方向的旋转因子矩阵；利用平面阵列的互质理论，消除角度模糊，求解阵列的方位角和俯仰角。本发明实现了互质面阵模型下俯仰角和方位角的低复杂、高精度、无模糊联合估计。

权利要求

1.基于互质面阵的二维波达方向快速估计方法，其特征在于，包括以下步骤：

步骤1：根据互质面阵模型，分x轴和y轴构造阵列流型矩阵；所述互质面阵模型由两个二维均匀稀疏子阵组合而成；

步骤2：分别求解各子阵接收信号的协方差矩阵，并分x轴和y轴方向构造阵列的传播算子矩阵；

步骤3：在对阵列流型进行分块处理的基础上采用PM算法，分别求取各子阵沿x轴和y轴方向的旋转因子矩阵；

步骤4：利用平面阵列的互质理论，消除角度模糊，求解阵列的方位角和俯仰角。

2.根据权利要求1所述的基于互质面阵的二维波达方向快速估计方法，其特征在于，所述两个二维均匀稀疏子阵分别为子阵1和子阵2，其中子阵1的阵元间距为Md，子阵2的阵元间距为Nd，M、N互为质数，d＝λ/2，λ为入射信号波长。

3.根据权利要求1所述的基于互质面阵的二维波达方向快速估计方法，其特征在于，所述步骤1包括：

步骤1.1：构造各子阵的x轴阵列流型矩阵：

阵元间距为d的x轴阵列流型矩阵为：

其中，Ax为y轴阵列流型矩阵，N′r为x轴上均匀分布的阵元数，D为远场窄带信号以平面波的方式入射到阵列的个数，分别为来波方向；θi∈(-π,π)，分别为第i个入射信号的方位角和俯仰角；

步骤1.2：构造各子阵的y轴阵列流型矩阵：

阵元间距为d的y轴阵列流型矩阵为：

其中，Ay为y轴阵列流型矩阵，N′y为y轴上均匀分布的阵元数。

4.根据权利要求1所述的基于互质面阵的二维波达方向快速估计方法，其特征在于，所述步骤2包括：

步骤2.1：分别求解各子阵x轴和y轴接收信号的协方差矩阵；

步骤2.2：在x轴方向构造子阵1的传播算子矩阵：

其中，为x轴接收信号的协方差矩阵R1x的前D列，为子阵1的阵元数，阵元编号为

步骤2.3：以步骤2.2方式在y轴方向构造子阵1的传播算子矩阵：

步骤2.4：以步骤2.2方式在x轴方向构造子阵2的传播算子矩阵；

步骤2.5：以步骤2.3方式在y轴方向构造子阵2的传播算子矩阵。

5.基于权利要求4所述的基于互质面阵的二维波达方向快速估计方法，其特征在于，所述子阵1沿x轴接收信号为：

其中，s(k)为发送信号向量，n(k)是功率为的加性高斯白噪声向量，k为快拍数，K为最大快拍数，k∈{1,2…K}；

子阵1沿y轴接收信号为：

6.根据权利要求1所述的基于互质面阵的二维波达方向快速估计方法，其特征在于，所述步骤3包括：

所述子阵沿x轴方向的旋转因子矩阵的求解过程为：

步骤3.1：对于子阵1，根据x轴接收信号矩阵，得到：

其中，代表矩阵Pc1x的前Nr(Nr-1)行，代表矩阵Pc1x的后Nr(Nr-1)行；

步骤3.2：对进行特征值分解，得到的特征值与Φ1x的对角线元素相对应，从而可以求得子阵1沿x轴方向的旋转因子矩阵Φ1x；

步骤3.3：以步骤3.1、步骤3.2方式求得子阵1沿y轴方向的旋转因子矩阵Φ1y；

步骤3.4：以步骤3.1、步骤3.2方式求得子阵2沿x轴方向的旋转因子矩阵Φ2x；

步骤3.5：以步骤3.3方式求得子阵2沿y轴方向的旋转因子矩阵Φ2y。

7.根据权利要求2所述的基于互质面阵的二维波达方向快速估计方法，其特征在于，所述阵列的方位角和俯仰角为：

当M＝1时：

当M＞1时：

其中，

其中，θi为阵列的方位角，为阵列的俯仰角，α1和β1分别为子阵1沿x轴方向和沿y轴方向的旋转因子矩阵的相位，α2和β2分别为子阵2沿x轴方向和沿y轴方向的旋转因子矩阵的相位。

说明书

技术领域

本发明属于阵列信号处理技术领域，尤其涉及基于互质面阵的二维波达方向快速估计方法。

背景技术

二维波达方向估计(direction-of-arrival，DOA)是获取目标信号位置信息的关键技术，其广泛应用于雷达，声呐，射电天文学等方面。基于阵列信号处理的二维波达方向估计技术是一种被动定位技术，能够在不发射测试信号和不需要求解发射信号先验信息的条件下获取目标信号的方位角和俯仰角。目前基于阵列的二维波达方向估计技术主要采用三种阵型，即：L型阵列，圆形阵列和平面方阵(简称为面阵)。基于L型阵列的波达方向估计技术，计算复杂度较低，无需进行参数配对，且可以产生渐近无偏估计的效果，但该方法对来波方向的变化较为敏感，鲁棒性差，同等条件下的角度估计精度没有平面阵高。采用均匀圆阵进行二维波达方向估计，该算法首先进行波束空间转换，将均匀圆阵转化为线阵模型，然后利用旋转不变参数估计技术(Estimation of Signal Parameters Via RotationalInvarianceTechniques，ESPRIT)进行二维波达方向估计，精度较高，且不存在估计“模糊”问题，但圆阵存在先天不足，即不能够进行二维相干信号的有效估计。

目前基于面阵的二维波达方向估计主要建立在均匀平面阵基础上，估计方法主要有多重信号分类(Multiple Signal Classification，MUSIC)算法，二维Capon算法，二维ESPRIT算法和二维传播算子(Propagator Method，PM)方法。采用均匀面阵的二维估计算法，其中MUSIC方法估计精度较高，且属于无偏估计，但是计算复杂度高；二维Capon算法，二维ESPRIT算法在MUSIC算法的模型基础上牺牲少量精度来降低运算复杂度，但二维Capon算法角度分辨率较低，二维ESPRIT算法需要多次子空间分解，样本数较大时，计算复杂度依然较高，且精度无法保证。传统的非稀疏均匀阵列受限于天线尺寸，阵元之间互耦效应等因素的影响，估计精度和角度分辨率较低。

发明内容

本发明的目的在于克服上述二维波达方向估计算法中存在的不足，提出了基于互质面阵的二维波达方向快速估计方法，实现了互质面阵模型下俯仰角和方位角的低复杂、高精度、无模糊联合估计。

为了实现上述目的，本发明采用以下技术方案：

基于互质面阵的二维波达方向快速估计方法，包括以下步骤：

步骤1：根据互质面阵模型，分x轴和y轴构造阵列流型矩阵；所述互质面阵模型由两个二维均匀稀疏子阵组合而成；

步骤2：分别求解各子阵接收信号的协方差矩阵，并分x轴和y轴方向构造阵列的传播算子矩阵；

步骤3：在对阵列流型进行分块处理的基础上采用PM算法，分别求取各子阵沿x轴和y轴方向的旋转因子矩阵；

步骤4：利用平面阵列的互质理论，消除角度模糊，求解阵列的方位角和俯仰角。

优选地，所述两个二维均匀稀疏子阵分别为子阵1和子阵2，其中子阵1的阵元间距为Md，子阵2的阵元间距为Nd，M、N互为质数，d＝λ/2，λ为入射信号波长。

优选地，所述步骤1包括：

步骤1.1：构造各子阵的x轴阵列流型矩阵：

阵元间距为d的x轴阵列流型矩阵为：

其中，Ax为y轴阵列流型矩阵，Nr′为x轴上均匀分布的阵元数，D为远场窄带信号以平面波的方式入射到阵列的个数， 分别为来波方向；θi∈(-π,π)， 分别为第i个入射信号的方位角和俯仰角；

步骤1.2：构造各子阵的y轴阵列流型矩阵：

阵元间距为d的y轴阵列流型矩阵为：

其中，Ay为y轴阵列流型矩阵，Ny′为y轴上均匀分布的阵元数。

优选地，所述步骤2包括：

步骤2.1：分别求解互质面阵x轴和y轴接收信号的协方差矩阵；

步骤2.2：在x轴方向构造子阵1的传播算子矩阵：

其中， 为x轴接收信号的协方差矩阵R1x的前D列， 为子阵1的阵元数，阵元编号为

步骤2.3：以步骤2.2方式在y轴方向构造子阵1的传播算子矩阵：

步骤2.4：以步骤2.2方式在x轴方向构造子阵2的传播算子矩阵；

步骤2.5：以步骤2.3方式在y轴方向构造子阵2的传播算子矩阵。

优选地，所述子阵1沿x轴接收信号为：

其中，s(k)为发送信号向量，n(k)是功率为 的加性高斯白噪声向量，k为快拍数，K为最大快拍数，k∈{1,2…K}；

子阵1沿y轴接收信号为：

优选地，所述步骤3包括：

所述子阵沿x轴方向的旋转因子矩阵的求解过程为：

步骤3.1：对于子阵1，根据x轴接收信号矩阵，得到：

其中， 代表矩阵Pc1x的前Nr(Nr-1)行， 代表矩阵Pc1x的后Nr(Nr-1)行；

步骤3.2：对 进行特征值分解，得到的特征值与Φ1x的对角线元素相对应，从而可以求得子阵1沿x轴方向的旋转因子矩阵Φ1x；

步骤3.3：以步骤3.1、步骤3.2方式求得子阵1沿y轴方向的旋转因子矩阵Φ1y；

步骤3.4：以步骤3.1、步骤3.2方式求得子阵2沿x轴方向的旋转因子矩阵Φ2x；

步骤3.5：以步骤3.3方式求得子阵2沿y轴方向的旋转因子矩阵Φ2y。

优选地，所述阵列的方位角和俯仰角为：

当M＝1时：

当M>1时：

其中，

其中，θi为阵列的方位角， 为阵列的俯仰角，a1和β1分别为子阵1沿x轴方向和沿y轴方向的旋转因子矩阵的相位，a2和β2分别为子阵2沿x轴方向和沿y轴方向的旋转因子矩阵的相位。

与现有技术相比，本发明具有的有益效果：

本发明首先构造互质平面阵模型，然后根据接收信号的协方差求解传播算子矩阵，并利用传播算子矩阵进行两次阵列流型重构，解算旋转因子矩阵，最后根据子阵阵元间距互质的特性消除稀疏阵列的角度模糊，确定目标信号的俯仰角和方位角。本发明在互质面阵模型基础上，采用双向传播算子的二维波达方向估计方法，替代原始算法的子空间分解和谱峰搜索，实现了互质面阵模型下俯仰角和方位角的低复杂、高精度、无模糊联合估计。

互质阵列属于特殊的稀疏线阵，阵元间距大于半波长，互耦效应显著下降，分辨率和估计精度得到有效提高，但会出现“伪峰”现象。本发明采用两个均匀稀疏阵列组合成互质阵列进行二维波达方向估计时，若阵元间距数“互质”，就能保证二维波达方向估计中“真峰”位置相互重叠，而“伪峰”被去除掉。

本发明采用的PM算法只需要进行少次低维子空间分解且不需谱峰搜索，降低了运算复杂度，采用的互质阵列由于其采用稀疏模型，阵列特性得到极大改善，互质阵列阵元间距大于半波长，互耦效应显著下降，阵列孔径和阵列自由度显著提高，分辨率和检测精度也得到了改善。将互质阵列引入到平面阵型进行二维波达方向估计，估计精度大大提高。

附图说明

图1为本发明基于互质面阵的二维波达方向快速估计方法的基本流程示意图。

图2为本发明基于互质面阵的二维波达方向快速估计方法的互质面阵模型示意图。

具体实施方式

下面结合附图和具体的实施例对本发明做进一步的解释说明：

实施例一：

如图1所示，本发明的基于互质面阵的二维波达方向快速估计方法，包括以下步骤：

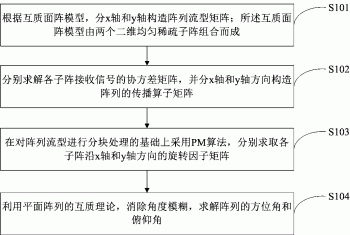
步骤S101：根据互质面阵模型，分x轴和y轴构造阵列流型矩阵；所述互质面阵模型由两个二维均匀稀疏子阵组合而成；

所述步骤S101包括：

步骤S1011：构造各子阵的x轴阵列流型矩阵；

步骤S1012：构造各子阵的y轴阵列流型矩阵。

所述步骤S101具体如下：

二维面阵接收阵元数为Nr′×Nr′，阵元间距为d，d＝λ/2，λ为入射信号波长，第k个阵元相对参考阵元位置为(xk,yk,zk)。假设有D个远场窄带信号以平面波的方式入射到阵列，来波方向分别为 入射功率 θi∈(-π,π)， 其为第i个入射信号的方位角和俯仰角。根据几何关系，空间第k个阵元相对于(0,0,0)位置的波程差为：

平面阵列中，取zk＝0，上式简化为

在平面阵列中，x轴上均匀分布有Nr′个阵元，阵列流型记为Ax，则

相应的y轴上Nr′个阵元的阵列流型记为Ay

整个阵列的接收信号表示为

x(k)＝As(k)+n(k)(7)

x(k)为接收信号向量，s(k)为发送信号向量，n(k)是功率为 的加性高斯白噪声向量，k为快拍数，K为最大快拍数，k∈{1,2…K}，A是阵列流型

互质平面阵是在二维均匀面阵的基础上发展而来，它由两个二维均匀稀疏面阵组合而成，分别为子阵1和子阵2，互质面阵的典型形式如图2所示，假设两个子阵的阵元数分别为 和 阵元间距为Md和Nd，M、N互为质数，两个子阵的第一个阵元重合，故整个阵列含有 个阵元，为了表述方便，令Nr＝Nr1＝Nr2。

按照上述方式，构造子阵1和子阵2的x轴、y轴阵列流型矩阵A1x、A1y、A2x、A2y。

步骤S102：分别求解各子阵接收信号的协方差矩阵，并分x轴和y轴方向构造阵列的传播算子矩阵；

所述步骤S102包括：

步骤S1021：分别求解互质面阵x轴和y轴接收信号的协方差矩阵；

步骤S1022：在x轴方向构造子阵1的传播算子矩阵：

步骤S1023：在y轴方向构造子阵1的传播算子矩阵：

步骤S1024：在x轴方向构造子阵2的传播算子矩阵；

步骤S1025：在y轴方向构造子阵2的传播算子矩阵。

步骤S102具体如下：

互质面阵可以看成两个均匀阵列的叠加，对于单个均匀阵列，例如子阵1，上式(8)也可以写成如下形式

其中， 代表平行于x轴的第i列子阵阵列流型，即相当于将二维阵列按照x轴进行向量化。

根据阵列结构， 和 存在如下关系

称Φ1x为沿x轴方向的旋转因子矩阵。

相应的将二维阵列按照y轴进行向量化，得到

因而接收信号表示为

首先将阵列流型矩阵A1x进行分块处理

为A1x的前D行，即 为D×D阶矩阵。设

称 为传播算子矩阵。求接收信号x1x的协方差矩阵 并进行分块处理

为自相关矩阵R1x的前D列，当处于无噪声理想条件下时， 因此传播算子矩阵可以转化为如下形式

解算上式得到

同理，可求得互质面阵接收信号x1y、x2x、x2y的协方差矩阵R1y、R2x及R2y；子阵1在y轴方向构造阵列的传播算子矩阵

子阵2在x轴和y轴方向构造阵列的传播算子矩阵 和

步骤S103：在对阵列流型进行分块处理的基础上采用PM算法，分别求取各子阵沿x轴和y轴方向的旋转因子矩阵；

所述步骤S103包括：

步骤S1031：求得子阵1沿x轴方向的旋转因子矩阵Φ1x；

步骤S1032：求得子阵1沿y轴方向的旋转因子矩阵Φ1y；

步骤S1033：求得子阵2沿x轴方向的旋转因子矩阵Φ2x；

步骤S1034：求得子阵2沿y轴方向的旋转因子矩阵Φ2y。

所述步骤S203具体如下：

对于子阵1，构造 根据式(18)、(19)

定义

代表矩阵Pc1x的前Nr(Nr-1)行， 代表矩阵Pc1x的后Nr(Nr-1)行。根据式(11)(14)可以得到

结合式(23)-(27)，有如下关系式

并且依据式(28)-(30)，所以

整理得到

对 进行特征值分解，得到的特征值与Φ1x的对角线元素相对应，从而可以求得旋转因子矩阵Φ1x。根据式(17)可以得到类似于(32)的形式，进而求得子阵1沿y轴方向的旋转因子矩阵Φ1y。

同理，可求得子阵2沿x轴和y轴方向的旋转因子矩阵Φ2x及Φ2y。

步骤S104：利用平面阵列的互质理论，消除角度模糊，求解阵列的方位角和俯仰角；

所述步骤S104具体如下：

对于子阵1，取矩阵Φ1x和Φ1y的相位，表示为：

当M＝1，根据式(34)约束条件得到k11＝k12＝0，利用式(33)求得方位角和俯仰角如下：

当M>1时，求子阵2的旋转因子矩阵Φ2x和Φ2y的相位α2和β2：

根据互质阵列的特性，采用本实施例算法进行来波方向估计时，不存在角度模糊的问题，针对k11，k21，k12，k22取值范围内的可能值，进行俯仰角和方位角的估计如下：

最终得到方位角和俯仰角：

值得说明的是，互质平面阵列中采用旋转不变PM算法进行二维波达方向估计时，不存在角度模糊问题，即公式(33)和(37)中的参数k11，k21，k12，k22具有唯一性，证明过程如下：

根据公式(33)和公式(37)得到

整理上式得到

Na1-Ma2＝2Nk11π-2Mk21π(44)

因为M，N，k11，k21均为整数，所以令2kπ＝2Nk11π-2Mk21π，由此得到

Na1-Mα2＝2kπ (45)

当k＝0，则

结合式(33)和式(37)中k11，k21的范围，-(M+1)/2<k11<(M+1)/2，-(N+1)/2<k21<(N+1)/2。以及M，N互质的特性得到k11＝k21＝0。

当k≠0，假设存在模糊角度 满足

联合式(33)，得到

同理，利用子阵2可以得到类似的关系式

由此可得

因为-(M+1)/2<k11,k′11<(M+1)/2，-(N+1)/2<k21,k′21<(N+1)/2，所以-M≤k11-k′11≤M，-N≤k21-k′21≤N，若要等号成立，则必须满足k11＝k′11，k21＝k′21或k11-k′11＝±M，k21-k′21＝±N。

当k11＝k′11，k21＝k′21时， 模糊不存在，此时假设不成立，即互质平面阵解算得到的来波方向不存在角度模糊。

当k11-k′11＝±M，k21-k′21＝±N时，分M为偶数和M为奇数两种情况进行讨论。

若M为偶数，根据k11，k′11的取值范围，则

设 从而

显然不成立，即k11-k′11≠±M。

若M为奇数，则 或 不妨设 推导得到

显然与式(34)相矛盾，所以k11-k′11≠±M。

综上M为偶数和奇数两种情况，得到k11-k′11＝±M不成立，因此只能存在k11＝k′11，k21＝k′21的情况，所以 与 为同一个角度，从而证明了互质平面阵列模型下不存在角度模糊的问题。

以上所示仅是本发明的优选实施方式，应当指出，对于本技术领域的普通技术人员来说，在不脱离本发明原理的前提下，还可以做出若干改进和润饰，这些改进和润饰也应视为本发明的保护范围。

基于互质面阵的二维波达方向快速估计方法专利购买费用说明

Q：办理专利转让的流程及所需资料

A：专利权人变更需要办理著录项目变更手续，有代理机构的，变更手续应当由代理机构办理。

1：专利变更应当使用专利局统一制作的“著录项目变更申报书”提出。

2：按规定缴纳著录项目变更手续费。

3：同时提交相关证明文件原件。

4：专利权转移的，变更后的专利权人委托新专利代理机构的，应当提交变更后的全体专利申请人签字或者盖章的委托书。

Q:专利著录项目变更费用如何缴交

A：（1）直接到国家知识产权局受理大厅收费窗口缴纳,（2）通过代办处缴纳，（3）通过邮局或者银行汇款,更多缴纳方式

Q：专利转让变更，多久能出结果

A：著录项目变更请求书递交后，一般1-2个月左右就会收到通知，国家知识产权局会下达《转让手续合格通知书》。