专利摘要
本发明属于光学检测装置领域,并具体公开了一种偏振调制结构及偏振测量系统,其包括旋转补偿器和偏振器,所述旋转补偿器为连续旋转的复合波片,该复合波片由多个同种材料的单波片组合而成,该复合波片的整体结构由各单波片的厚度和光轴夹角依据偏振特性传递矩阵优化设计确定。本发明的偏振调制结构具有结构简单,容易加工,波长适用范围广的优点,并且基于该偏振调制结构可设计出宽波段偏振测量系统,适应于宽波段精密偏振测量的需求。
权利要求
1.一种偏振调制结构,其特征在于,包括旋转补偿器和偏振器,所述旋转补偿器为连续旋转的复合波片,该复合波片由多个同种材料的单波片组合而成,该复合波片的整体结构由各单波片的厚度和光轴夹角依据偏振特性传递矩阵优化设计确定。
2.如权利要求1所述的偏振调制结构,其特征在于,在依据偏振特性传递矩阵优化设计确定复合波片的整体结构的过程中,其依据的准则为使偏振特性传递矩阵在其适用波段范围内具有最小的奇异性。
3.如权利要求2所述的偏振调制结构,其特征在于,在适用波段范围内具有最小的奇异性优选为在适用波段范围内矩阵最大奇异性最小、在适用波段范围内矩阵的平均奇异性最小或在适用波段范围内矩阵的奇异性均方差最小。
4.如权利要求1-3任一项所述的偏振调制结构,其特征在于,复合波片的整体结构由各单波片的厚度和光轴夹角依据偏振特性传递矩阵优化设计确定,具体包括如下步骤:
(1)确定偏振调制结构的适用波长范围Γ,复合波片制作材料,单波片个数N;选择复合波片中单波片厚度变化范围Ω和光轴夹角变化范围Θ;
(2)分别在厚度变化范围Ω和光轴夹角变化范围Θ中选择N个单波片的厚度值[d
(3)根据选择的单波片的厚度值和光轴夹角值建立偏振调制结构的偏振特性传递矩阵D(λ),然后计算偏振调制结构的偏振特性传递矩阵D(λ)在波长范围Γ内的最大奇异性ζ
其中,τ(λ)为与波长λ相关的系数,ζ表示矩阵奇异性的评价标准;
(4)重复步骤(2)-(3),使偏振调制结构的偏振特性传递矩阵在波长范围Γ内的最大奇异性ζ
5.如权利要求4所述的偏振调制结构,其特征在于,所述偏振特性传递矩阵D(λ)采用如下公式计算:
D(λ)=f{[δ
其中,f为由偏振调制结构偏振传递特性确定的函数关系,P为偏振器透光轴方位角,δ
6.如权利要求4或5所述的偏振调制结构,其特征在于,所述相位延迟量由各单波片的厚度确定:
其中,δ
7.如权利要求5或6所述的偏振调制结构,其特征在于,光轴方位角由光轴夹角和参考单波片光轴方位角确定:
θ
其中,θ
8.一种偏振测量系统,其特征在于,至少包含一个如权利要求1-7任一项所述的偏振调制结构。
9.如权利要求8所述的偏振测量系统,其特征在于,所述偏振测量系统中的器件及偏振光的偏振特性采用穆勒矩阵或斯托克斯向量表示。
10.如权利要求8或9所述的偏振测量系统,其特征在于,所述偏振测量系统为单旋转补偿器椭偏仪、双旋转补偿器椭偏仪或旋转补偿器斯托克斯偏振仪。
说明书
技术领域
本发明属于光学检测装置领域,更具体地,涉及一种偏振调制结构及偏振测量系统。
背景技术
偏振测量系统包括椭偏仪和偏振仪,是一类重要的光学测量仪器,通过探测偏振光与样品相互作用(反射或透射)后的偏振态或偏振态改变量,来获取待测对象的光学特性或其他参数,如光学常数、几何尺寸、形貌分布等,在物理、化学、材料、生物、天文、海洋、遥感、导航等多个领域都有着广泛的应用。偏振测量系统实现偏振测量的关键在于偏振器件对偏振光的调制与解调,根据偏振调制器件工作原理的不同,偏振测量系统可以分为不同的种类。常用的偏振调制器件包括偏振器、液晶相位延迟器、光弹调制器、旋转补偿器等。其中,旋转补偿器通过旋转电机或其他装置带动光学补偿器连续旋转实现偏振调制与解调,由于能够实现全偏振态调制,且具有调制精度和稳定性高、适用光谱范围宽、安装调整与校准简单等优点,是目前偏振测量系统中主要的偏振调制器件。
常用的旋转补偿器类型包括波片、菲涅耳棱镜。其中,菲涅尔棱镜利用全反射相变原理使偏振光产生相位差,能够很好地实现紫外-红外波段的偏振调制与解调,但其结构复杂,调整难度大,且具有光学二向色等。相比而言,波片通常由双折射晶体材料制作而成,通过材料本身的双折射特性使偏振光产生相位差,波片尺寸紧凑、结构简单、调整容易,且没有二向色等缺陷,是一种比较理想的偏振调制器件。单个双折射晶体片构成的单波片是最简单的一种波片,但是由于双折射材料色散特性,单波片的适用波长范围非常窄。通常的做法是将若干片同种材料或不同材料单波片组合成复合波片,以降低单波片的加工难度或色散特性。
常见复合波片包括Beckers波片(J.M.Beckers,Appl.Opt.,Vol.10,pp.973-975,1971)和Pancharatnam波片(S.Pancharatnam,Proc.Indian.Acad.Sci.A,Vol.41,pp.137-144,1955)。Beckers波片是由不同材料单波片组成的复合波片,利用不同材料光学特性相互抵消部分色散,但这种复合波片的消色差特性取决于所选用的材料,消色差适用波长范围依然有限。Pancharatnam波片是用奇数个(大于等于3个)同种材料的单波片组成的消色差复合波片,其消色差特性由各单波片的个数和结构确定,但是这种复合波片的结构具有严格的对称性要求,中间的波片为半波长波片,以中间半波片为参考,两边对称位置的单波片要求具有相同的相位延迟量和光轴方位,这种复杂的结构增加了加工难度,极大地限制了其消色差适用波段范围。另外,还有将上述两种消色差复合波片结合而成的超级消色差复合波片(P.Hariharan,J.Mod.Opt.,Vol.51,pp.2315-2322,2004),可以在很宽的波长范围内实现消色差效果,但是这种复合波片要求至少包括两种材料的6个单波片,而且要求具有对称性结构,这极大地增加了加工难度和成本,也会在偏振测量系统中引入更多误差。上述复合波片由于消色差适用波长范围有限或结构过于复杂难以加工,在实际偏振测量系统中应用很少。
发明内容
针对现有技术的以上缺陷或改进需求,本发明提供了一种偏振调制结构及偏振测量系统,其通过设计基于复合波片旋转补偿器结合偏振器的偏振调制基本单元,并依据偏振调制结构的偏振特性传递矩阵优化设计确定基于复合波片旋转补偿器的整体结构,设计获得的偏振调制结构具有结构简单,容易加工,波长适用范围广的优点,并且基于该偏振调制结构可设计出宽波段偏振测量系统,适应于宽波段精密偏振测量的需求。
为实现上述目的,按照本发明的一个方面,提出了一种偏振调制结构,包括旋转补偿器和偏振器,所述旋转补偿器为连续旋转的复合波片,该复合波片由多个同种材料的单波片组合而成,该复合波片的整体结构由各单波片的厚度和光轴夹角依据偏振特性传递矩阵优化设计确定。
作为进一步优选的,在依据偏振特性传递矩阵优化设计确定复合波片的整体结构的过程中,其依据的准则为使偏振特性传递矩阵在其适用波段范围内具有最小的奇异性。
作为进一步优选的,在适用波段范围内具有最小的奇异性优选为在适用波段范围内矩阵最大奇异性最小、在适用波段范围内矩阵的平均奇异性最小或在适用波段范围内矩阵的奇异性均方差最小。
作为进一步优选的,复合波片的整体结构由各单波片的厚度和光轴夹角依据偏振特性传递矩阵优化设计确定,具体包括如下步骤:
(1)确定偏振调制结构的适用波长范围Γ,复合波片制作材料,单波片个数N;选择复合波片中单波片厚度变化范围Ω和光轴夹角变化范围Θ;
(2)分别在厚度变化范围Ω和光轴夹角变化范围Θ中选择N个单波片的厚度值[d1,d2,...,dN]和光轴夹角值[Δθ1,Δθ2,...,ΔθN];
(3)根据选择的单波片的厚度值和光轴夹角值建立偏振调制结构的偏振特性传递矩阵D(λ),然后计算偏振调制结构的偏振特性传递矩阵D(λ)在波长范围Γ内的最大奇异性ζmax:
其中,τ(λ)为与波长λ相关的系数,ζ表示矩阵奇异性的评价标准;
(4)重复步骤(2)-(3),使偏振调制结构的偏振特性传递矩阵在波长范围Γ内的最大奇异性ζmax最小,此时对应的复合波片各单波片的厚度值和光轴夹角值即为复合波片的整体结构参数。
作为进一步优选的,所述偏振特性传递矩阵D(λ)采用如下公式计算:
D(λ)=f{[δ1(λ),δ2(λ),…,δN(λ)];[θ1(λ),θ2(λ),…,θN(λ)];P}
其中,f为由偏振调制结构偏振传递特性确定的函数关系,P为偏振器透光轴方位角,δ1(λ),δ2(λ),…,δN(λ)分别表示第1,2,…,N个单波片的相位延迟量,θ1(λ),θ2(λ),…,θN(λ)分别表示第1,2,…,N个单波片的光轴方位角。
作为进一步优选的,所述相位延迟量由各单波片的厚度确定:
其中,δn(λ)为第n个单波片的相位延迟量,dn为第n个单波片的厚度,λ为工作波长,λ∈Γ,Δn(λ)为波长λ下波片制作材料的双折射率。
作为进一步优选的,光轴方位角由光轴夹角和参考单波片光轴方位角确定:
θn(λ)=θN0+Δθn,
其中,θn(λ)为第n个单波片的光轴方位角,Δθn为第n个单波片光轴与参考单波片光轴间的夹角,θN0为参考单波片的光轴方位角。
按照本发明的另一方面,提供了一种偏振测量系统,至少包含一个所述的偏振调制结构。
作为进一步优选的,所述偏振测量系统中的器件及偏振光的偏振特性采用穆勒矩阵或斯托克斯向量表示,其中器件即为偏振测量系统中的旋转补偿器和偏振器,偏振光为各器件的入射光与出射光。
作为进一步优选的,所述偏振测量系统为单旋转补偿器椭偏仪、双旋转补偿器椭偏仪或旋转补偿器斯托克斯偏振仪。
总体而言,通过本发明所构思的以上技术方案与现有技术相比,主要具备以下的技术优点:
1.本发明研究设计了基于复合波片的旋转补偿器+偏振器的偏振调制结构,其可作为一个偏振调制基本单元应用至偏振测量系统中,该基于复合波片的旋转补偿器为复合波片,由多个同种材料的单波片组合而成,其整体结构由各单波片的厚度和光轴夹角确定,对复合波片的具体结构和各单波片的厚度、光轴夹角等没有做限定,为复合波片的偏振调制性能优化提供更多自由度。
2.本发明的偏振调制结构的系统参数,包括偏振器的方位角、复合波片各单波片的厚度和光轴夹角,通过偏振调制结构的偏振特性传递矩阵优化设计得到,从而可以优化复合波片的整体结构,使偏振测量系统在更宽的波长范围内具有最优的偏振调制性能,适应更宽波段精密偏振测量的需求。
3.本发明还提供了偏振测量系统,其包括基于复合波片旋转补偿器+偏振器组成的偏振调制基本单元,该基于复合波片的旋转补偿器作为核心偏振调制器件,使得偏振测量系统的光路调节方便、系统校准简单、能够适应更宽的波长范围,适应于宽波段(例如可以设计出覆盖200-1700nm波段范围的宽波段偏振测量系统)精密偏振测量的需求。
附图说明
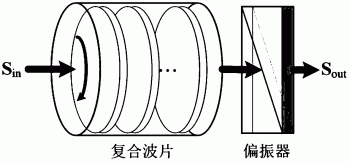
图1是本发明实施例提供的一种偏振调制结构的示意图;
图2是本发明实施例提供的复合波片的结构示意图;
图3a-c是本发明优化设计的包含4个氟化镁单波片的复合波片旋转补偿器在设计波长范围200-1700nm内的等效偏振特征参数的光谱曲线;其中,a为等效相位延迟量的光谱曲线,b为等效光轴方位角的光谱曲线,c为等效旋光角的光谱曲线;
图4是基于本发明所设计的包含4个氟化镁单波片的复合波片旋转补偿器的偏振调制基本单元在设计波长范围200-1700nm内的偏振特性传递矩阵2-范数条件数的光谱曲线;
图5a-d是各类典型的基于复合波片旋转补偿器的偏振测量系统的结构示意图。
具体实施方式
为了使本发明的目的、技术方案及优点更加清楚明白,以下结合附图及实施例,对本发明进行进一步详细说明。应当理解,此处所描述的具体实施例仅仅用以解释本发明,并不用于限定本发明。此外,下面所描述的本发明各个实施方式中所涉及到的技术特征只要彼此之间未构成冲突就可以相互组合。
如图1所示,本发明实施例提供的一种偏振调制结构(即偏振调制基本单元),其包括旋转补偿器和偏振器,旋转补偿器和偏振器前后依次设置,偏振器的透光轴方位角预先设定,且在偏振调制结构工作过程中固定不变,旋转补偿器为连续旋转的复合波片,该复合波片(即旋转补偿器)由多个同种材料的单波片组合而成,该复合波片的整体结构由各单波片的厚度和光轴夹角依据偏振调制结构的偏振特性传递矩阵优化设计确定,即复合波片整体结构由各单波片的厚度和光轴夹角唯一确定,各单波片的厚度和光轴夹角又依据偏振调制结构的偏振特性传递矩阵优化设计确定。
具体而言,在依据偏振调制结构的偏振特性传递矩阵优化设计确定复合波片的整体结构的过程中,其依据的准则为使偏振调制结构的偏振特性传递矩阵在其适用波段范围内具有最小的奇异性,该适用波段根据所设计的偏振测量系统的具体应用情况进行选择。其中,在适用波段范围内具有最小的奇异性优选为在适用波段范围内矩阵最大奇异性最小或在适用波段范围内矩阵的平均奇异性最小或在适用波段范围内矩阵的奇异性均方差最小。
上述偏振调制结构的偏振传递特性可以用下式描述:
Sout=MP·MC·Sin (1)
式中,Sin和Sout分别表示入射偏振调制结构和从偏振调制结构出射的偏振光的斯托克斯向量,MP和MC分别为偏振器和旋转补偿器的穆勒矩阵;
其中,偏振器的穆勒矩阵MP由下式计算:
式中,P表示偏振器的透光轴方位角。
上述复合波片是N个同种材料的单波片组合而成的一个整体,由各单波片的厚度和光轴间的夹角确定其整体结构。复合波片的结构如图2所示,沿光线传播方向,各单波片依次被标记为1,2,…,N,Fn和θn表示第n个单波片的光轴及其方位角,第n个单波片的厚度为dn,其中n=1,2,…,N。选择第一个单波片光轴作为参考轴,各单波片光轴与第一个单波片光轴间的夹角为Δθn=θn–θ1,其中n=1,2,…,N。在旋转过程中,复合波片作为一个整体,其各单波片的厚度dn和光轴间的夹角Δθn不会发生变化。
复合波片的琼斯矩阵U可以根据各个单波片的厚度dn和光轴方位角θn计算获得,具体依据下式计算:
式中,u11、u12、u21和u22为复合波片的琼斯矩阵的元素,δn和θn分别为第n(n=1,2,…,N)个单波片的相位延迟量和光轴方位角,i为虚数单位,其中,δn可以由下式计算:
式中,dn为第n个单波片的厚度,λ为复合波片的工作波长,Δn(λ)为波长λ下波片材料的双折射率,可以查阅资料获得。
根据琼斯等效理论,复合波片的偏振特性可以用等效相位延迟量δe、等效光轴方位角θe和等效旋光角ρe三个等效偏振特征参数描述,其琼斯矩阵U还可以用下式描述:
联立式(3)-(5)便可以求得复合波片的各等效偏振特征参数在不同波长λ下的值,具体如下
其中,Im表示复数的虚部,Re表示复数的实部。
因此,上述基于复合波片的旋转补偿器的穆勒矩阵MC可以由下式计算得到:
其中,θt=θe+ωt表示基于复合波片的旋转补偿器在任意时刻t时的光轴方位角,ω为复合波片的旋转角速率。
将式(2)和式(7)代入式(1)中,可计算偏振测量系统光强探测器处探测的光强,即偏振调制结构的出射偏振光斯托克斯向量的第一个元素Sout(1),具体表达式如下:
I(t)=Sout(1)=a0+a2mcos(2mωt+Φ2m)+b2msin(2mωt+Φ2m)(8)
其中,a0,(a2m,b2m)为傅里叶系数直流分量和归一化交流分量,Φ2m=2mθe为相位函数,其中m=1,2表示傅里叶系数级次,ω为复合波片的旋转角速率,t为旋转时间。
各傅里叶系数的具体表达式如下:
a2=0·S1+0·S2+0·S3+sin(δe)sin(2P′)·S4(9b)
b2=0·S1+0·S2+0·S3-sin(δe)cos(2P′)·S4(9c)
式中,Si(i=1,2,3,4)是偏振调制结构的入射偏振光斯托克斯向量Sin的第i个元素,这里P'=P+ρe为偏振器透光轴方位角P中耦合了复合波片旋转补偿器的等效旋光角ρe。
对偏振测量系统光强探测器实际探测到的光强信号进行傅里叶变换得到的表达式如下:
I′(t)=Sout(1)=a′0+a′2mcos(2mωt)+b2′msin(2mωt)(10)
式中,a'0,(a'2m,b'2m)为实际探测光强信号的傅里叶系数直流分量和归一化交流分量,其中m=1,2表示傅里叶系数级次。各傅里叶系数间具有如下关系:
a′0=a0(11a)
a′2m=a2mcosΦ2m-b2msinΦ2m(11b)
b2′m=a2msinΦ2m+a2mcosΦ2m(11c)
优选地利用光谱仪进行光强探测,光谱仪适用波段范围应覆盖偏振测量系统的适用波长范围,当光强探测器为光谱仪时,探测信号为式(10)给出的光强信号在一段时间内的积分,通常在旋转补偿器的光学周期T=π/ω内进行K次采集,每段积分时间区间为[(k-1)π/(Kω),kπ/(Kω)],其中k=1,2,…,K。为保证偏振测量系统能够获得稳定的解,在一个光学周期内光强信号采集次数K应大于等于偏振测量系统待测的偏振参数个数。
光谱仪探测到的光强信号gk的具体表达式为:
上式可以改写为矩阵形式
G=D·Sin(13)
其中,G=[g1,g2,…,gK]
通过上述式(13)即可推导出D,其为常规的数学运算,在此不赘述。推导出的D是由复合波片等效相位延迟量δe、等效光轴方位角θe、等效旋光角ρe和偏振器透光轴方位角P等系统参数组成的K×4阶矩阵。
本发明用偏振特性传递矩阵D的奇异性来评估偏振调制结构以及包含该偏振调制结构的偏振测量系统抵抗噪声和误差的能力,偏振特性传递矩阵D越远离奇异,说明式(13)所示的线性方程的解越稳定,偏振测量系统对噪声和误差的抵抗能力越强,反之则偏振测量系统对噪声和误差的抵抗能力越弱。即本发明在依据偏振调制结构的偏振特性传递矩阵优化设计确定各单波片的厚度和光轴夹角的过程中,其依据的准则为使偏振调制结构的偏振特性传递矩阵在其适用波段范围内具有最小的奇异性。而在适用波段范围内具有最小的奇异性优选为在适用波段范围内矩阵最大奇异性最小或在适用波段范围内矩阵的平均奇异性最小或在适用波段范围内矩阵的奇异性均方差最小。
矩阵的奇异性可以用矩阵的条件数、奇异值、特征值等参数定量评定,为使本发明内容更便于理解,此处利用条件数评定方法举例说明。偏振调制结构的偏振特性传递矩阵D的条件数可以用下式计算
κp(D)=||D||p||D
其中,D
由式(8)-(13)可知,基于复合波片旋转补偿器的偏振调制结构的偏振特性传递矩阵D最终由复合波片等效相位延迟量δe、等效光轴方位角θe、等效旋光角ρe以及偏振器的透光轴方位角P确定。由于复合波片等效相位延迟量δe、等效光轴方位角θe、等效旋光角ρe都具有色散特性,是波长λ的函数,因此,基于复合波片旋转补偿器的偏振调制结构的偏振特性传递矩阵D也随波长λ变化,进而偏振特性传递矩阵D的奇异性也随波长λ变化。由前所述可知,本发明的复合波片的等效相位延迟量δe、等效光轴方位角θe、等效旋光角ρe等偏振特征参数由其整体结构和材料特性确定,而其整体结构由各单波片的厚度d=[d1,d2,...,dN]和光轴间的夹角Δθ=[Δθ1,Δθ2,...,ΔθN]确定。为了使本发明的基于复合波片的旋转补偿器偏振测量系统在宽波长范围内具有较强的噪声和误差抵抗能力等性能,本发明利用依据偏振调制结构的偏振特性传递矩阵D对复合波片的整体结构进行优化设计,使复合波片各单波片具有最优的厚度和光轴夹角,使偏振调制结构的偏振特性传递矩阵D在所要求的波长范围Γ内的最大奇异性最小,从而使基于该复合波片的旋转补偿器偏振测量系统在波长范围Γ内具有最优的噪声和误差抵抗能力等性能。
当使用条件数作为评定矩阵奇异性标准时,复合波片的整体结构可以依据如下式所示的形式作为优化设计准则:
式中,τ(λ)是一个随波长变化的系数,d=[d1,d2,...,dN]和Δθ=[Δθ1,Δθ2,...,ΔθN]分别表示复合波片各单波片的厚度值的集合和光轴夹角的集合,do=[d1o,d2o,…,dNo]和Δθo=[Δθ1o,Δθ2o,...,ΔθNo]分别表示复合波片各单波片的厚度优化设计值的集合和光轴夹角优化设计值的集合,Ω和Θ分别表示复合波片中单波片的厚度变化范围和光轴夹角变化范围,arg表示优化设计过程,min表示在一定范围内选取目标函数的最小值,max表示在一定范围内选取目标函数的最大值。
因此,式(15)表示的优化设计过程可以描述为:在偏振测量系统适用波长范围Γ、复合波片各单波片厚度变化范围Ω和光轴夹角变化范围Θ内,使偏振调制结构的偏振特性传递矩阵的条件数的最大值最小的复合波片各单波片的厚度值和光轴夹角值即为优化设计的复合波片整体结构参数。
具体而言,复合波片的整体结构采用如下步骤确定:
(1)确定偏振调制结构的适用波长范围Γ,确定复合波片的制作材料和单波片个数N,选择复合波片中单波片厚度变化范围Ω和光轴夹角变化范围Θ,上述参数均可根据实际需要进行选择与确定;
(2)分别在厚度变化范围Ω和光轴夹角变化范围Θ中选择N个单波片的厚度值[d1,d2,...,dn,...,dN]和光轴夹角值[Δθ1,Δθ2,...,Δθn,...,ΔθN],其中,dn为第n(n=1,2,…,N)个单波片的厚度值,Δθn为第n(n=1,2,…,N)个单波片的光轴与参考单波片光轴之间的夹角,例如选择第N0(1≤N0≤N)个单波片作为参考单波片,则ΔθN0=0,参考单波片可根据实际需要进行选择;
(3)根据选择的单波片的厚度值和光轴夹角值建立偏振调制结构的偏振特性传递矩阵D(λ),然后计算偏振特性传递矩阵D(λ)在波长范围Γ内的最大奇异性ζmax:
其中,τ(λ)为与波长λ相关的系数,一般取1;ζ表示矩阵奇异性的评价标准,例如用矩阵的条件数、奇异值或特征值作为评价标准,具体可根据实际需要选择具体的评价标准,其为现有技术,在此不赘述;
偏振特性传递矩阵D(λ)由式(8)-(13)确定,可以表示为如下形式:
D(λ)=f{[δ1(λ),δ2(λ),…,δN(λ)];[θ1(λ),θ2(λ),…,θN(λ)];P}
其中,f为由偏振调制结构偏振传递特性确定的函数关系,具体由光强探测器的光强探测方式确定,P为偏振器透光轴方位角,δ1(λ),δ2(λ),…,δn(λ),…,δN(λ)分别表示第1,2,…,n,…,N个单波片的相位延迟量,θ1(λ),θ2(λ),…,θn(λ),…,θN(λ)分别表示第1,2,…,n,…,N个单波片的光轴方位角;
相位延迟量由各单波片的厚度确定:
其中,δn(λ)为第n(n=1,2,…,N)个单波片的相位延迟量,dn为第n个单波片的厚度值,λ为复合波片的工作波长,λ∈Γ,Δn(λ)为波长λ下波片制作材料的双折射率;
光轴方位角由光轴夹角和参考单波片光轴方位角确定:
θn(λ)=θN0+Δθn,
其中,θn(λ)为第n(n=1,2,…,N)个单波片的光轴方位角,Δθn为第n个单波片光轴与参考单波片光轴间的夹角,θN0为参考单波片的光轴方位角。
(4)重复步骤(2)-(3),使偏振调制结构的偏振特性传递矩阵在波长范围Γ内的最大奇异性ζmax最小,此时对应的复合波片各单波片的厚度值和光轴夹角值即为复合波片的整体结构参数,即在厚度变化范围Ω和光轴夹角变化范围Θ中重新选择复合波片各单波片的厚度值和光轴夹角值,直至步骤(2)中选择的复合波片各单波片的厚度值和光轴夹角值遍历厚度变化范围Ω和光轴夹角变化范围Θ,使偏振特性传递矩阵在波长范围Γ内的最大奇异性ζmax最小,此时对应的复合波片各单波片的厚度值[d1o,d2o,…,dNo]和光轴夹角值[Δθ1o,Δθ2o,...,ΔθNo]确定为复合波片的整体结构参数。
对于复合波片而言,选用的制作材料的透光波长范围应覆盖偏振测量系统的适用波长范围Γ,包括但不限于石英、氟化镁、方解石、云母、石膏或蓝宝石,复合波片中的单波片可以是单个双折射晶体片,也可以是两个双折射晶体片按快轴正交组成。当复合波片中的单波片为单个双折射晶体片时,其厚度和光轴方位角由该双折射晶体片的厚度和光轴方位角确定;当复合波片中的单波片为两个双折射晶体片组成时,该复合波片的厚度由两个双折射晶体片的厚度之差确定,该单波片的光轴方位角由其中较厚双折射晶体片的光轴方位角确定。通过将本发明的偏振调制结构作为基本单元可以构建至少包含一个所述偏振调制结构的偏振测量系统,为了便于光强的测定,该偏振测量系统还配备有光强探测器。
为了使本发明内容更容易理解和实施,下面以适用于200-1700nm波长范围的基于复合波片的偏振测量系统的设计为一个具体实施例,详细说明本发明内容的具体实施过程。
(1)选定偏振测量系统适用波长范围Γ,具体的根据偏振测量系统宽波段测量需求要求,选择覆盖紫外-可见-红外的200-1700nm波长范围作为所要设计的偏振测量系统的适用波长范围,即Γ=[200nm,1700nm];
(2)选择偏振器和光强探测器,其适用波长范围应覆盖第(1)所选择的波长范围Γ,本实施例选用洛凶棱镜偏振片和光谱仪分别作为偏振测量系统的偏振器和光强探测器;
(3)确定复合波片的整体结构,具体依据以下步骤进行:
3.1)选择复合波片制作材料和复合波片中单波片的个数N,所选用的材料的透光波长范围覆盖第(1)步所选择的波长范围Γ;单波片个数N应该综合考虑波片的制作难度和偏振测量系统适用波长范围确定,本实施例选用氟化镁作为波片的制作材料,单波片个数选为N=4;
3.2)选择复合波片中单波片的厚度变化范围Ω和光轴夹角变化范围Θ,本实施例选定氟化镁单波片的厚度和光轴夹角变化范围分别为Ω=[0,100μm]和Ω=[0,90°];
3.3)在第3.2)步选择的厚度变化范围Ω和光轴夹角变化范围Θ中任意选择一组复合波片各单波片的厚度值[d1,d2,d3,d4]和光轴夹角值[Δθ1,Δθ2,Δθ3,Δθ4],其中,dn和Δθn为第n(n=1,2,3,4)个单波片的厚度值和其光轴与参考单波片光轴之间的夹角值,为叙述方便,本实施例选择第1个单波片作为参考波片,Δθ1=0;
3.4)计算基于复合波片旋转补偿器的偏振调制基本单元的系统参数:首先,任意给定复合波片中第1个单波片的光轴方位角θ1和偏振器的透光轴方位角P(光轴方位角θ1和偏振器的透光轴方位角P这两个参数可以参与优化也可以不参与优化,本实施例中这两个参数不优化,即给定后始终不变);接着,计算复合波片各单波片的相位延迟量δn和光轴方位角θn,其中,相位延迟量δn可以根据各单波片的厚度dn、波长λ以及氟化镁的双折射率Δn(λ)计算得到,具体依据式(4)计算;而光轴方位角则可以由第1个单波片的光轴方位角θ1和光轴间夹角Δθn计算得到,θn=θ1+Δθn;最后,根据复合波片各单波片的相位延迟量δn和光轴方位角θn可以获得复合波片的等效相位延迟量δe、等效光轴方位角θe和等效旋光角ρe,具体依据式(3)-(6)进行。
3.5)计算基于复合波片旋转补偿器的偏振调制基本单元的偏振特性传递矩阵D:根据偏振调制基本单元的系统参数,包括复合波片的等效相位延迟量δe、等效光轴方位角θe、等效旋光角ρe和偏振器的透光轴方位角P等,依据式(8)-(13)可以计算获得随波长λ变化的偏振调制基本单元的偏振特性传递矩阵D(λ),为确保基于复合波片的旋转补偿器偏振测量系统求解的稳定性,本实施例中光谱仪在一个光学周期内光强采集个数取为K=50;
3.6)计算偏振调制基本单元的偏振特性传递矩阵D(λ)在第(2)步所选择的波长范围Γ内的最大奇异性 其中,ζ表示矩阵奇异性的评价标准,τ(λ)为与波长λ相关的系数,当以条件数为矩阵奇异性评价标准时,ζ=κp,在本实施例中选择2-范数计算矩阵条件数,即p=2,具体依据式(14)进行计算,令τ(λ)≡1,可以计算获得在波长范围Γ内偏振调制基本单元的偏振特性传递矩阵D的最大2-范数条件数κ2max;
3.7)重复第3.3)-3.6)步,即在第(2)步选择的厚度变化范围Ω和光轴夹角变化范围Θ中重新选择一组不同的复合波片各单波片的厚度值[d1',d2',d3',d4']和光轴夹角值[Δθ1',Δθ2',Δθ3',Δθ4'],继续进行计算,直至复合波片各单波片厚度值和光轴夹角值分别遍历完其相应变化范围Ω和Θ,从所有获得的偏振调制基本单元的偏振特性传递矩阵D(λ)在波长范围Γ内的最大条件数中选取其最小值,其对应的复合波片各单波片的厚度值和光轴夹角值即为最终优化设计的复合波片的整体结构参数。本实施例中,包含4个氟化镁单波片的复合波片的整体结构参数最终优化设计结果为:各单波片厚度值[33.58μm,13.28μm,13.49μm,20.21μm]和光轴间夹角值为[0,67.9°,46.4°,14.9°]。该复合波片的等效相位延迟量、等效光轴方位角和等效旋光角的等效偏振特征参数的光谱曲线如图3a-c所示。基于该复合波片旋转补偿器的偏振调制基本单元的偏振特性传递矩阵2-范数条件数曲线如图4所示。
3.8)根据上述确定的结构参数加工所需的波片,并依据实际加工难度、成本、误差容许范围等因素,确定复合波片中各个单波片是选择复合零级波片还是真零级波片,具体地,本发明实例中所有的氟化镁单波片均采用真零级波片形式;
(4)根据具体的偏振测量系统配置,选择光源、样品台、旋转组件、控制器、计算机等,并设计相应机械支撑部件和控制系统,进而构建基于复合波片的旋转补偿器偏振测量系统。
图5给出了几种典型的基于复合波片的旋转补偿器偏振测量系统,包括双旋转复合波片穆勒矩阵椭偏仪(图5a)、单旋转复合波片椭偏仪配置一(图5b)、单旋转复合波片椭偏仪配置二(图5c)和旋转复合波片斯托克斯偏振仪(图5d)等。但是,本发明的基于复合波片的旋转补偿器偏振测量系统是一类系统,并不止于上述几种具体的配置,任何包含本发明所述基于复合波片的旋转补偿器+偏振器组成的偏振调制基本单元的偏振测量系统均属于本发明保护范围。
上述实施例基于复合波片的旋转补偿器偏振测量系统的设计过程时仅以适用200-1700nm波段范围、包含4个氟化镁单波片的复合波片的旋转补偿器偏振测量系统的设计过程为一个具体实施例阐述本发明的基于复合波片的旋转补偿器偏振测量系统的设计实施步骤,但本发明不仅局限于上述具体实施方式,本领域一般技术人员根据本发明公开的设计方法,可以采用其他多种具体实施方式实施本发明,如选择不同的波段范围、选用不同的波片制作材料和不同的单波片个数、采用其他矩阵奇异性评价标准等,因此,凡在本发明的精神和原则之内所作的任何修改、等同替换和改进等,均应包含在本发明的保护范围之内。
一种偏振调制结构及偏振测量系统专利购买费用说明
![]()
Q:办理专利转让的流程及所需资料
A:专利权人变更需要办理著录项目变更手续,有代理机构的,变更手续应当由代理机构办理。
1:专利变更应当使用专利局统一制作的“著录项目变更申报书”提出。
2:按规定缴纳著录项目变更手续费。
3:同时提交相关证明文件原件。
4:专利权转移的,变更后的专利权人委托新专利代理机构的,应当提交变更后的全体专利申请人签字或者盖章的委托书。
Q:专利著录项目变更费用如何缴交
A:(1)直接到国家知识产权局受理大厅收费窗口缴纳,(2)通过代办处缴纳,(3)通过邮局或者银行汇款,更多缴纳方式
Q:专利转让变更,多久能出结果
A:著录项目变更请求书递交后,一般1-2个月左右就会收到通知,国家知识产权局会下达《转让手续合格通知书》。
动态评分
0.0