专利摘要

本发明公开了一种飞行控制系统自适应调参方法，在设计过程中飞行控制系统结构固定，在飞行包线大幅变化情况下，通过建立飞行控制系统未知参数与闭环系统极点间的约束关系，实现飞行控制系统的鲁棒自适应调参。在设计过程中，首先依据飞行器模型的带宽频率，延迟时间，幅值裕度和相位裕度等飞行品质进行相应的性能约束，构建满足飞行性能要求的区域，然后再利用保护映射理论，获取满足区域稳定要求的飞行控制系统的设计参数，同时自动生成满足要求的控制器集合，实现控制系统的自适应调参。更为重要的是，调参过程中既可以对单参数进行调节，也可以实现多参数的协调综合设计，满足飞行控制系统多目标的设计参数整定需求。

权利要求

1.一种飞行控制系统自适应调参方法，其特征在于，包括下列步骤：

步骤一：初始化飞行控制系统，其控制律的表达式为：

$\Delta {\delta }_e=K_z^{\theta }\mathrm{\Delta \theta }+K_z^{\stackrel{·}{\theta }}\Delta \stackrel{·}{\theta }+K_z^h(\mathrm{\Delta h}-{\mathrm{\Delta h}}_g)+K_z^{\stackrel{·}{h}}\Delta \stackrel{·}{h}$

其中，Δθ和 分别表示飞行器的俯仰角偏差及其变化率;Δh和 表示飞行器的高度偏差及其变化率;Δδ_e表示飞行器的舵面偏转角;Δh_g为飞行器高度指令信号; 为需要整定的控制参数；

步骤二：设置综合飞行控制系统与飞机模型的闭环控制系统的设计目标为：

极点最大的实部α_t≤-1；

短周期极点最小的阻尼比ξ_t≥0.6；

短周期最大自然频率ω_t≤10；

Ω_t=Ω(α_t,ξ_t,ω_t)作为目标区域；

步骤三：

选择未知增益参数集合K_j(j=1,...,p)（K∈R^P），设置 作为初始值，结合步骤二中的设计目标区域，得到迭代区域：求取步骤二所述闭环控制系统状态矩阵A(f(K⁰))的特征值Λ={λ₁,λ₂,...,λ_n}，判断是否均处于目标区域Ω_t内，若完全在内，则满足控制目标要求，即初值是符合控制要求的精确增益参数值，停止搜索；如果不完全在目标区域Ω_t内，则判断A(f(K⁰))是否为稳定系统，即判断是否有右半平面的极点，若有,则仅由稳定裕度α和自然频率ω两个参数约束,定义区域Ω_Λ为包含稳定矩阵A所有特征值的最小区域，即Λ∈Γ_Λ，区域Γ_Λ=Γ(α_Λ,ω_Λ)唯一定义，其中α_Λ=max{Re(λ_i)}和ω_Λ=max{|λ_i|}；结合目标区域,可以定义迭代区域Γ_U=Γ(α_U,ω_U)，其中α_U=α_Λ，ω_U=max{ω_t,ω_Λ}；否则,稳定区域Ω由(α,ξ,ω)进行约束,定义区域Ω_Λ是包含矩阵A所有特征值的最小区域，即Λ∈Ω_Λ，且区域Ω_Λ=Ω(α_Λ,ξ_Λ,ω_Λ)唯一定义，其中α_Λ=max{α_t,α_Λ}，ξ_Λ=min{ξ(λ_i)}ω_Λ=max{|λ_i|}；结合目标区域,可以定义迭代区域Ω_U=Ω(α_U,ξ_U,ω_U)，其中α_U=max{α_t,α_Λ}，ξ_U＝min{ξ_t,ξ_Λ}ω_U=max{ω_t,ω_Λ}；

依据定义迭代区域，设定闭环控制系统的稳定集合为：

$S\left({\Omega }_U\right)=\{A\left(K^0\right)\in R^{n\times n}:\sigma \left(A\left(K^0\right)\right)⋐{\Omega }_U\}$

σ(A)是矩阵A的特征值；

所述迭代区域内三个参数的保护映射关系为：

$v_{\alpha }\left(A\left(f\left(K^0\right)\right)\right)=\det (A{\left(f\left(K^0\right)\right)}^2/-{\alpha }_U/\otimes /)\det (A\left(f\left(K^0\right)\right)-{\alpha }_U/)$

$v_{\xi }\left(A\left(f\left(K^0\right)\right)\right)=\det \left(A\left(f\left(K^0\right)\right)\right)·\det (A{\left(f\left(K^0\right)\right)}^2\otimes /+(1-{{2\xi }_U}^2)A\left(f\left(K^0\right)\right)\otimes A\left(f\left(K^0\right)\right))$

$\begin{array}{c}{v}_{\omega }\left(A\left(f\left(K^0\right)\right)\right)=\det (A\left(f\left(K^0\right)\right)\otimes A\left(f\left(K^0\right)\right)-{{\omega }_U}^2/\otimes /)·\\ \det (A\left(f\left(K^0\right)\right)-{\omega }_U/)\det (A\left(f\left(K^0\right)\right)+{\omega }_U/)\end{array}$

其中，v_α,ν_ξ,ν_ω分别表示迭代区域所对应的保护映射关系；A(f(K⁰))为飞行器闭环控制系统的状态空间矩阵；det为矩阵A(f(K⁰))的行列式；I表示单位阵； 表示矩阵的Bialternate积；

步骤四：求取闭环控制系统状态矩阵A(f(K⁰))的特征值，判断是否均处于目标区域Ω_t内，若完全在内，则满足控制目标要求，即初值是符合控制要求的精确增益参数值，停止搜索；如果不完全在目标区域Ω_t内，则进行步骤五；

步骤五：按照保护映射理论,根据飞行控制系统多目标的设计参数整定实际需求，依据飞行模型中存有的单变量或双变量，分别应用单参数或双参数算法，选择整定过程，迭代出一组新的增益参数值K'；

步骤六：根据步骤五得到的迭代的新的增益参数值，和迭代前的参数值，依据||K^m-K^m+1||≤ε_K(1+||K^m||)进行的判定，其中ε_K是一个适当小的正数值，若该式不满足，继续回到步骤五，将K'作为初值来进行迭代,得到新的参数值；若该式满足，则计算A(f(K′))的特征值，判断是否均处于目标区域Ω_t内，若完全在内，则满足控制目标要求，即初值是符合控制要求的精确增益参数值，停止搜索；如果不完全在目标区域Ω_t内，则返回步骤三,重新定义迭代区域,完成参数整定过程；

步骤七：用步骤六新的增益参数值得到闭环控制系统状态矩阵A(f(K))中，验证控制系统的指标值是否符合控制的设计目标要求，如符合控制的设计目标要求，则结束。

2.如权利要求1所述的飞行控制系统自适应调参方法，其特征在于，所述的步骤五中，单参数整定过程为：

若飞行器模型为与单个模型参数a相关，即综合飞行控制系统与飞机模型的闭环控制系统可写为(A(a),B(a),C(a),D(a))；针对系统状态矩阵A(a)，若控制器结构和增益参数值固定，可以得到模型变参数a最大的鲁棒自适应区域；

a^-≈sup{a<a₀:v_Ω[A(a)]=0}(若不存在，值为-∞)

a⁺≈inf{a>a₀:v_Ω[A(a)]=0}(若不存在，值为+∞)

且a∈(a^-,a⁺)是非奇异矩阵A(a)在a=a₀处的最大的鲁棒自适应区域；

设置线性变参数模型的初始环境条件，即a=a₀=a_min，此时控制对象为固定的运动模型，获取满足目标区域Ω的增益向量初值K⁰；

当增益向量K=K⁰，将K⁰带入原控制系统状态矩阵A（a,K）中，此时的情况为控制器结构和增益参数值固定，得到的保护映射表达式所含的未知参数为模型参数a，找到模型满足控制要求的最大的鲁棒自适应稳定区域 这样，对于在 范围内的任意a值处的运动模型，K⁰均可保证控制系统是相对于Ω区域稳定的；初始增益向量K⁰以及保护映射确定稳定区域的边界，寻找新的增益向量K¹，使得闭环系统极点严格分部在Ω目标区域内部；根据这个新得到的增益向量，可以得到新的最大鲁棒自适应稳定区域 其中 然后重复上述过程，直到对所有的a∈[a_min,a_max]都找到相应的稳定控制器K'，即新的增益参数值。

3.如权利要求1所述的飞行控制系统自适应调参方法，其特征在于，所述的步骤五中，双参数整定过程为：

令综合飞行控制系统与飞机模型的闭环控制系统A(r₁,r₂,K)中K=[K_i]为增益向量，Ω是目标稳定区域，目的为找到一个与参数r₁和r₂相关的控制器K(r₁,r₂)，保证控制系统的所有极点都在Ω稳定区域内；

首先固定r₂=r_2,0=r_2,min，利用单参数增益调度算法得到一个在区间[r_1,min,r_1,max]内稳定的控制器K⁰(r₁),然后找到包含r_2，0的最大开区间 因此，这个控制器K⁰(r₁)在 范围内使控制系统稳定；令 然后在[r_1,min,r_1,max]内再次搜索寻找到新的控制器K¹(r₁)，确保控制系统在 重复多次进行上述过程，直至覆盖整个操作区域，最后得到控制参数K'，即新的增益参数值。

说明书

技术领域

本发明涉及一种飞行器控制方法，尤其是一种运用保护映射理论来设计飞行控制系统的自动调参方法，完成控制系统参数的自适应整定。

背景技术

由于现代飞行控制系统的要求越来越高，传统方法已经不能满足其复杂的应用要求，综合多目标要求实现飞行控制系统参数的自适应调节显得十分必要。传统飞行控制系统调参中最为常用的方法有两种，第一种形式是利用在平衡点附近给定的线性化模型，设计出相应的一组线性控制器进行合成，这些控制器插值的预置变量，可能是内生变量，也可能是外生变量。第二种形式是基于线性变参数（LPV）技术，即将控制系统调参问题转换成计算线性矩阵不等式最优的问题，控制参数直接从设计的LPV方程里获取。然而，当动态补偿器或执行机构被考虑的时候，第一种形式的插值则成为了一个具有挑战性的问题，更为重要的是其稳定性无法得以证明。而第二种形式又使得控制系统设计过于保守，尤其当操作区域变大时，可能会导致不可达的优化问题，难以实现闭环系统的全局稳定性。

为了改进飞行控制系统参数的自适应整定方法，兼顾插值调参和LPV调参的优点，避免二者的缺点，本发明提出基于保护映射理论的飞行控制系统自适应调参算法。该算法能依据给定的性能指标，实现飞行控制系统参数的自适应整定。与经典的增益调度方法不同，它的设计过程不需基于多平衡点，只需要给定一个初始控制器，然后自动寻找新的控制器，直到满足其他平衡点对稳定性的要求，覆盖整个工作区域。另一方面，该算法优于LPV的地方在于它可以使用给定的固定控制器，自动生成一组新的控制器，性能强大并且能覆盖整个工作域。此外，由于具有相同的飞行控制系统结构，很容易地实现插值调参，或者直接制定出查找表，极易满足工程的实际应用需求。

发明内容

技术问题

本发明要解决的技术问题是提供一种基于保护映射理论的飞行控制系统自适应调参方法，用于解决现代飞行控制系统的参数自适应整定问题，其利用保护映射理论，建立飞行控制系统未知增益参数与闭环控制系统极点间的约束关系，实现对飞行控制系统的参数自适应调节，确保飞行过程的全局稳定性。

技术方案

为了实现飞行控制系统的自适应调参，本发明基于保护映射理论提出了一种新的飞行控制系统控制自适应调参数方法。设计过程中飞行控制系统结构固定，在飞行包线大幅变化情况下，通过建立飞行控制系统未知参数与闭环系统极点间的约束关系，实现飞行控制系统的鲁棒自适应调参。在设计过程中，首先依据飞行器模型的带宽频率，延迟时间，幅值裕度和相位裕度等飞行品质进行相应的性能约束，构建满足飞行性能要求的区域，然后再利用保护映射理论，获取满足Ω区域稳定要求的飞行控制系统的设计参数，同时自动生成满足要求的控制器集合，实现控制系统的自适应调参。更为重要的是，调参过程中既可以对单参数进行调节，也可以实现多参数的协调综合设计，满足飞行控制系统多目标的设计参数整定需求。具体步骤如下：

步骤一：初始化飞行控制系统，其控制律的表达式为：

Δδe=KzθΔθ+Kzθ·Δθ·+Kzh(Δh-Δhg)+Kzh·Δh·]]>

其中，Δθ和 分别表示飞行器的俯仰角偏差及其变化率;Δh和 表示飞行器的高度偏差及其变化率;Δδ_e表示飞行器的舵面偏转角;Δh_g为飞行器高度指令信号; 为需要整定的控制参数；

步骤二：设置综合飞行控制系统与飞机模型的闭环控制系统的设计目标为：

极点最大的实部α_t≤-1；

短周期极点最小的阻尼比ξ_t≥0.6；

短周期最大自然频率ω_t≤10；

Ω_t=Ω(α_t,ξ_t,ω_t)作为目标区域；

步骤三：

选择未知增益参数集合K_j(j=1,...,p)（K∈R^P），设置 作为初始值，结合步骤二中的设计目标区域，得到迭代区域：求取步骤二所述闭环控制系统状态矩阵A(f(K⁰))的特征值Λ={λ₁,λ₂,...,λ_n}，判断是否均处于目标区域Ω_t内，若完全在内，则满足控制目标要求，即初值是符合控制要求的精确增益参数值，停止搜索；如果不完全在目标区域Ω_t内，则判断A(f(K⁰))是否为稳定系统，即判断是否有右半平面的极点，若有,则仅由稳定裕度α和自然频率ω两个参数约束,定义区域Ω_Λ为包含稳定矩阵A所有特征值的最小区域，即Λ∈Γ_Λ，区域Γ_Λ=Γ(α_Λ,ω_Λ)唯一定义，其中α_Λ=max{Re(λ_i)}和ω_Λ=max{|λ_i|}；结合目标区域,可以定义迭代区域Γ_U=Γ(α_U,ω_U)，其中α_U=α_Λ，ω_U=max{ω_t,ω_Λ}；否则,稳定区域Ω由(α,ξ,ω)进行约束,定义区域Ω_Λ是包含矩阵A所有特征值的最小区域，即Λ∈Ω_Λ，且区域Ω_Λ=Ω(α_Λ,ξ_Λ,ω_Λ)唯一定义，其中α_Λ=max{α_t,α_Λ}，ξ_Λ=min{ξ(λ_i)}ω_Λ=max{|λ_i|}；结合目标区域,可以定义迭代区域Ω_U=Ω(α_U,ξ_U,ω_U)，其中α_U=max{α_t,α_Λ}，ξ_U＝min{ξ_t,ξ_Λ}ω_U=max{ω_t,ω_Λ}；

依据定义迭代区域，定义闭环控制系统的稳定集合为：

S(ΩU)={A(K0)∈Rn×n:σ(A(K0))⋐ΩU}]]>

σ(A)是矩阵A的特征值；

所述迭代区域内三个参数的保护映射关系为：

vα(A(f(K0)))=det(A(f(K0))2/-αU/⊗/)det(A(f(K0))-αU/)]]>

vξ(A(f(K0)))=det(A(f(K0)))·det(A(f(K0))2⊗/+(1-2ξU2)A(f(K0))⊗A(f(K0)))]]>

vω(A(f(K0)))=det(A(f(K0))⊗A(f(K0))-ωU2/⊗/)·det(A(f(K0))-ωU/)det(A(f(K0))+ωU/)]]>

其中，v_α,ν_ξ,ν_ω分别表示迭代区域所对应的保护映射关系；A(f(K⁰))为飞行器闭环控制系统的状态空间矩阵；det为矩阵A(f(K⁰))的行列式；I表示单位阵； 表示矩阵的Bialternate积；

步骤四：求取闭环控制系统状态矩阵A(f(K⁰))的特征值，判断是否均处于目标区域Ω_t内，若完全在内，则满足控制目标要求，即初值是符合控制要求的精确增益参数值，停止搜索；如果不完全在目标区域Ω_t内，则进行步骤五；

步骤五：按照保护映射理论,根据飞行控制系统多目标的设计参数整定实际需求，依据飞行模型中存有的单变量或双变量，分别应用单参数或双参数算法，选择整定过程，迭代出一组新的增益参数值K'；

步骤六：根据步骤五得到的迭代的新的增益参数值，和迭代前的参数值，依据||K^m-K^m+1||≤ε_K(1+||K^m||)进行的判定，其中ε_K是一个适当小的正数值，若该式不满足，继续回到步骤五，将K'作为初值来进行迭代,得到新的参数值；若该式满足，则计算A(f(K′))的特征值，判断是否均处于目标区域Ω_t内，若完全在内，则满足控制目标要求，即初值是符合控制要求的精确增益参数值，停止搜索；如果不完全在目标区域Ω_t内，则返回步骤三,重新定义迭代区域,完成参数整定过程；

步骤七：用步骤六新的增益参数值得到闭环控制系统状态矩阵A(f(K))中，验证控制系统的指标值是否符合控制的设计目标要求，如符合控制的设计目标要求，则结束。

有益效果

本发明的方法有利于解决飞行控制系统中的参数自适应调节问题，在大包线的飞行环境下，依据设计所需的飞行品质和性能要求，通过选取初始的控制系统结构，基于保护映射理论自动地生产一组新的控制参数，性能强大且覆盖整个飞行区域，确保系统的全局稳定性。此外，由于具有相同的控制器结构，这些控制器能够快速地生成满足性能要求的多组控制系统增益，自适应地覆盖至所设定的飞行包线，亦能简单有效地完成控制系统的鲁棒性分析和研究，为工程的实际应用提供好的技术支持。

附图说明

图1为典型的飞行控制系统结构图；

图2为控制系统单参数整定流程图；

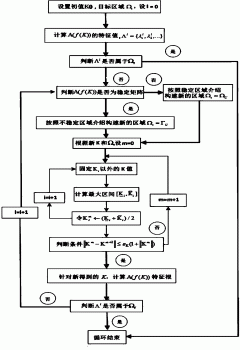
图3为飞行控制系统自适应参数整定流程图。

具体实施方式

以下结合附图对本发明的技术方案进行进一步说明。

本实施例选用典型的飞行控制系统，其结构如图1所示，其控制律的表达式可以写成：

Δδe=KzθΔθ+Kzθ·Δθ·+Kzh(Δh-Δhg)+Kzh·Δh·---(1)]]>

综合控制理论的知识，可以得到整个飞行控制系统的状态表达式。并进一步，设置控制系统的设计目标为：

1）极点最大的实部α_t≤-1。

2）短周期极点最小的阻尼比ξ_t≥0.6。

3）短周期最大自然频率ω_t≤10。

Ω_t=Ω(α_t,ξ_t,ω_t)作为目标区域.

选择未知增益参数集合K_j(j=1,...,p)（K∈R^P），设置 作为初始值.计算闭环控制系统状态矩阵A(f(K⁰))的特征值Λ={λ₁,λ₂,...,λ_n}，判断是否均处于目标区域Ω_t内，若完全在内，则满足控制目标要求，即初值是符合控制要求的精确增益参数值，停止搜索；如果不完全在目标区域Ω_t内，则判断A(f(K⁰))是否为稳定系统，即判断是否有右半平面的极点.若有,则仅由稳定裕度α和自然频率ω两个参数约束,定义区域Ω_Λ为包含稳定矩阵A所有特征值的最小区域，即Λ∈Γ_Λ，区域Γ_Λ=Γ(α_Λ,ω_Λ)唯一定义，其中α_Λ=max{Re(λ_i)}和ω_Λ=max{|λ_i|}。结合目标区域,可以定义迭代区域Γ_U=Γ(α_U,ω_U)，其中α_U=α_Λ，ω_U=max{ω_t,ω_Λ}。否则,稳定区域Ω由(α,ξ,ω)进行约束,定义区域Ω_Λ是包含矩阵A所有特征值的最小区域，即Λ∈Ω_Λ，且区域Ω_Λ=Ω(α_Λ,ξ_Λ,ω_Λ)唯一定义，其中α_Λ=max{α_t,α_Λ}，ξ_Λ=min{ξ(λ_i)}ω_Λ=max{|λ_i|}。结合目标区域,可以定义迭代区域Ω_U=Ω(α_U,ξ_U,ω_U)，其中α_U=max{α_t,α_Λ}，ξ_U＝min{ξ_t,ξ_Λ}ω_U=max{ω_t,ω_Λ}。

依据迭代区域,定义闭环控制系统的稳定集合为：

S(ΩU)={A(K0)∈Rn×n:σ(A(K0))⋐ΩU}---(2)]]>

σ(A)是矩阵A的特征值。

三个参数的保护映射关系为

vα(A(f(K0)))=det(A(f(K0))2/-αU/⊗/)det(A(f(K0))-αU/)---(3)]]>

vξ(A(f(K0)))=det(A(f(K0)))·det(A(f(K0))2⊗/+(1-2ξU2)A(f(K0))⊗A(f(K0)))---(4)]]>

vω(A(f(K0)))=det(A(f(K0))⊗A(f(K0))-ωU2/⊗/)·det(A(f(K0))-ωU/)det(A(f(K0))+ωU/)---(5)]]>

其中，v_α,ν_ξ,ν_ω分别表示迭代区域所对应的保护映射关系；A(f(K₀))为飞行器闭环控制系统的状态空间矩阵；det为矩阵A(f(K₀))的行列式；I表示单位阵； 表示矩阵的Bialternate积。

按照保护映射理论,进行单参数和双参数整定过程,具体为

（1）单参数整定过程

若飞行器模型为与单个模型参数a相关，即综合飞行控制系统与飞机模型的闭环控制系统可写为(A(a),B(a),C(a),D(a))；针对系统状态矩阵A(a)，若控制器结构和增益参数值固定，可以得到模型变参数a最大的鲁棒自适应区域；

a^-≈sup{a<a₀:v_Ω[A(a)]=0}(若不存在，值为-∞)

a⁺≈inf{a>a₀:v_Ω[A(a)]=0}(若不存在，值为+∞)

且a∈(a^-,a⁺)是非奇异矩阵A(a)在a=a₀处的最大的鲁棒自适应区域；

设置线性变参数模型的初始环境条件，即a=a₀=a_min，此时控制对象为固定的运动模型，获取满足目标区域Ω的增益向量初值K⁰。

当增益向量K=K⁰，将K⁰带入原控制系统状态矩阵A（a,K）中，此时的情况为控制器结构和增益参数值固定，得到的保护映射表达式所含的未知参数为模型参数a，找到模型满足控制要求的最大的鲁棒自适应稳定区域 这样，对于在 范围内的任意a值处的运动模型，K⁰均可保证控制系统是相对于Ω区域稳定的；初始增益向量K⁰以及保护映射确定稳定区域的边界，寻找新的增益向量K¹，使得闭环系统极点严格分部在Ω目标区域内部；根据这个新得到的增益向量，可以得到新的最大鲁棒自适应稳定区域 其中 然后重复上述过程，直到对所有的a∈[a_min,a_max]都找到相应的稳定控制器K'，即新的增益参数值。

（2）双参数整定过程

令综合飞行控制系统与飞机模型的闭环控制系统A(r₁,r₂,K)中K=[K_i]为增益向量，Ω是目标稳定区域，目的为找到一个与参数r₁和r₂相关的控制器K(r₁,r₂)，保证控制系统的所有极点都在Ω稳定区域内；

首先固定r₂=r_2,0=r_2,min，利用单参数增益调度算法得到一个在区间[r_1,min,r_1,max]内稳定的控制器K⁰(r₁),然后找到包含r_2,0的最大开区间 因此，这个控制器K⁰(r₁)在 范围内使控制系统稳定；令 然后在[r_1,min,r_1,max]内再次搜索寻找到新的控制器K¹(r₁)，确保控制系统在 重复多次进行上述过程，直至覆盖整个操作区域，最后得到控制参数K'，即新的增益参数值。

根据得到的迭代的新的增益参数值，和迭代前的参数值，依据||K^m-K^m+1||≤ε_K(1+||K^m||)进行的判定，其中ε_K是一个适当小的正数值，若该式不满足，继续将K'作为初值,按照保护映射理论,依据单参数和双参数整定过程来进行迭代,得到新的参数值；若该式满足，则计算A(f(K′))的特征值，判断是否均处于目标区域Ω_t内，若完全在内，则满足控制目标要求，即符合控制要求的精确增益参数值，停止搜索；如果不完全在目标区域Ω_t内,则将得到的增益参数作为初值,按照式(5)重新定义迭代区域,完成参数整定过程.

总的来说,根据上述单参数和双参数多项式矩阵应用，可以实现飞行控制系统多参数协调综合调参过程，其具体过程为：

步骤一：初始化飞行控制系统，其控制律的表达式为：

Δδe=KzθΔθ+Kzθ·Δθ·+Kzh(Δh-Δhg)+Kzh·Δh·]]>

其中，Δθ和 分别表示飞行器的俯仰角偏差及其变化率;Δh和 表示飞行器的高度偏差及其变化率;Δδ_e表示飞行器的舵面偏转角;Δh_g为飞行器高度指令信号; 为需要整定的控制参数.

步骤二：设置控制系统的设计目标为：

极点最大的实部α_t≤-1；

短周期极点最小的阻尼比ξ_t≥0.6；

短周期最大自然频率ω_t≤10；

Ω_t=Ω(α_t,ξ_t,ω_t)作为目标区域；

步骤三：

选择未知增益参数集合K_j(j=1,...,p)（K∈R^P），设置 作为初始值,结合设计目标区域,得到迭代区域.具体为:计算闭环控制系统状态矩阵A(f(K⁰))的特征值Λ={λ₁,λ₂,...,λ_n}，判断是否均处于目标区域Ω_t内，若完全在内，则满足控制目标要求，即初值是符合控制要求的精确增益参数值，停止搜索；如果不完全在目标区域Ω_t内，则判断A(f(K⁰))是否为稳定系统，即判断是否有右半平面的极点.若有,则仅由稳定裕度α和自然频率ω两个参数约束,定义区域Ω_Λ为包含稳定矩阵A所有特征值的最小区域，即Λ∈Γ_Λ，区域Γ_Λ=Γ(α_Λ,ω_Λ)唯一定义，其中α_Λ=max{Re(λ_i)}和ω_Λ=max{|λ_i|}。结合目标区域,可以定义迭代区域Γ_U=Γ(α_U,ω_U)，其中α_U=α_Λ，ω_U=max{ω_t,ω_Λ}。否则,稳定区域Ω由(α,ξ,ω)进行约束,定义区域Ω_Λ是包含矩阵A所有特征值的最小区域，即Λ∈Ω_Λ，且区域Ω_Λ=Ω(α_Λ,ξ_Λ,ω_Λ)唯一定义，其中α_Λ=max{α_t,α_Λ}，ξ_Λ=min{ξ(λ_i)}ω_Λ=max{|λ_i|}。结合目标区域,可以定义迭代区域Ω_U=Ω(α_U,ξ_U,ω_U)，其中α_U=max{α_t,α_Λ}，ξ_U＝min{ξ_t,ξ_Λ}ω_U=max{ω_t,ω_Λ}。

依据迭代区域,定义闭环控制系统的稳定集合为：

S(ΩU)={A(K0)∈Rn×n:σ(A(K0))⋐ΩU}]]>

σ(A)是矩阵A的特征值。

三个参数的保护映射关系为

vα(A(f(K0)))=det(A(f(K0))2/-αU/⊗/)det(A(f(K0))-αU/)]]>

vξ(A(f(K0)))=det(A(f(K0)))·det(A(f(K0))2⊗/+(1-2ξU2)A(f(K0))⊗A(f(K0)))]]>

vω(A(f(K0)))=det(A(f(K0))⊗A(f(K0))-ωU2/⊗/)·det(A(f(K0))-ωU/)det(A(f(K0))+ω

一种飞行控制系统自适应调参方法专利购买费用说明

Q：办理专利转让的流程及所需资料

A：专利权人变更需要办理著录项目变更手续，有代理机构的，变更手续应当由代理机构办理。

1：专利变更应当使用专利局统一制作的“著录项目变更申报书”提出。

2：按规定缴纳著录项目变更手续费。

3：同时提交相关证明文件原件。

4：专利权转移的，变更后的专利权人委托新专利代理机构的，应当提交变更后的全体专利申请人签字或者盖章的委托书。

Q:专利著录项目变更费用如何缴交

A：（1）直接到国家知识产权局受理大厅收费窗口缴纳,（2）通过代办处缴纳，（3）通过邮局或者银行汇款,更多缴纳方式

Q：专利转让变更，多久能出结果

A：著录项目变更请求书递交后，一般1-2个月左右就会收到通知，国家知识产权局会下达《转让手续合格通知书》。